[인공지능] AI - CS231n 1강, 2강 Image Classification pipeline

in CS Review on AI


AI 기초지식 쌓기

이번 연도는 나의 졸업 연도이다. 우리 학교는 졸업하려면 졸업 프로젝트라고 불리는 것을 해야 한다. 나는 평소에 관심이 있던 AI와 관련된 주제를 선택했고, 이를 위해서 다시 기본기를 쌓을 필요가 있었다. Stanford Univ.의 2017년 spring 강의 cs231n으로 기초적인 모델인 CNN, RNN 등을 배워볼 것이다. 추후 cs224n, cs231a, cs331, cs431 등을 공부할 생각이다.
덧붙인 사진과 code는 모두 cs231n의 강의자료를 참고했습니다.

cs231n youtube 강의 링크
cs231n 공개 강의자료
cs231n 과제 링크

CS231n 1강 - Intro. to CNN for Visual Recognition

컴퓨터 비전

컴퓨터가 마치 인간(생물)처럼 이미지를 식별하고 해석할 수 있도록 하는 연구 분야이다. CS, Math, Biology, Physics 등 다양한 학문이 결합되어 연구되고 있는 주제이다.

컴퓨터 비전의 역사

컴퓨터 비전에 지대한 영향을 끼친 연구들을 나열하자면 아래와 같다.

  • Hubel & Wiesel(1959)의 포유류 시각 매커니즘이란?
  • Larry Roberts(1963)의 우리가 보는 사물을 기하학적 모양으로 단순화(Block World)하여 특징점을 재구성
  • David Marr(1970)의 Hierarchical model이 제시(이미지의 특징 추출 및 특징에 따라 depth나 surface 추출하고 이를 토대로 3D modeling)
  • Brooks & Binford(1979)의 Generalized Cylinder
  • Fischler & Elschlager의 Pictorial Structure
  • Shi & Malik(1997)의 Normalized Cut(Object segmentation 시도)
  • David Lowe의 “SIFT” & Object Recognition
  • Viola & Jones(2001)의 Face Detection 더 있지만 너무 많아서 생략하겠다,,

CS231n 2강 - Image Classification pipeline

Keywords

  • k-NN ( K-Nearest Neighbors )
  • tensor
  • Semantic gap
  • Viewpoint variation / Illumination / Deformation / Occlusion / Background Clutter / Intraclass variation
  • Data-Driven Approach
  • Distance Metric ( L1 Distance / L2 Distance )
  • Hyperparameters
  • Train set / Validation set / Test set
  • Cross-Validation
  • Curse of dimensionality(차원의 저주)
  • Linear Classification
  • Score function

1. Image Classification은 어떻게 하는가?

냥!!

이미지 분류는 어떻게 이뤄질까..?

인간이라면 그냥 이미지를 보고 우리가 아는 것(??)이 그냥 튀어나온다!! 커여운 냐옹이쉑이군! 하지만 컴퓨터는 어떨까?? 컴퓨터는 그저 수많은 픽셀값의 나열로 받아들일 뿐이다. 이러한 차이를 Semantic Gap이라고 한다.

컴퓨터라면 아래와 같은 알고리즘으로 접근해볼 수 있다.

첫 번째로, 시스템엔 미리 정해 놓은 카테고리 집합이 있다고 하자. ex) 개, 고양이, 트럭, 비행기 등.. 이제 이러한 시스템에 위와 같은 이미지를 입력한다면 우리의 프로그램은 해당 이미지를 보고 어떤 카테고리에 속할지 판단하면 된다.

위의 일을 간단하게 고전적인 알고리즘을 짜듯이 접근해보자. 각각의 픽셀값을 따고 저장을 해서 대조해보는 식으로 코드를 짤 것인가..? 그 코드는 위의 단 하나의 사진만을 분류할 것이다. 이렇게 단순한 대조로는 아래와 같은 여러 문제가 발생한다.

  1. Viewpoint variation: 같은 고양이 사진임에도 바라보는 각도가 달라지면 위와 같은 픽셀값들은 완전히 달라진다. 사람은 인식하는 반면 컴퓨터는..
  2. Illumination: 조명이 달라진다면..?
  3. Deformation: 고양이 자체에 변형이 있다면..? 빵을 잘 굽지만, 항상 같은 자세는 아니니께,,
  4. Occlusion: 고양이 특으루다가 상자에 숨는 거 좋아하는데 어떻게 고양이인지 알까?
  5. Background Clutter: 배경색과 고양이가 비슷하다면?
  6. Intraclass variation: 고양이가 하나의 종만 있는 게 아니라 굉장히 다양한 종류가 있는데 어떻게?

정렬, RSA 등과 같은 알고리즘만을 다뤄봤던 우리는 위와 같은 분류기를 만들라고 하면 아마 한 줄도 작성하지 못할 것이다. 접근 방법 자체가 다르기 때문이다!! 그럼 어떻게 분류하려고 노력했을까?

처음 Hubel과 Wisel의 연구로 위 이미지에서 edge들을 따고 corner를 찾아냈다. 그 후, 고양이 인식을 위해 명시적인 규칙 집합을 만들어 분류하려 했으나 잘 안 되었다. 이 역시 픽셀값과 대조하는 것에서 크게 발전하지는 못했다고 생각한다. 왜냐면 객체마다 규칙 집합을 만들어줘야 해서 요구 메모리가 매우 클 것이다.

위와 같은 문제를 해결한 접근 방법은 바로 Data-Driven Approach이다. 말 그대로 데이터 중심으로 접근하는 것인데, 데이터 중심이라고 해서 위와 같이 데이터를 보고 규칙을 만드는 것이 아님!! 많은 데이터를 수집하고 Machine Learning 알고리즘을 통해 분류기를 학습시키고 새로운 이미지를 평가하면 된다. 바로 ML 개념이 나오긴 하지만 그냥 패스.. 다 알고 있다고 가정하자,,

2. Nearest Neighbor Algorithm & K-NN

어떤 데이터를 보고 그 데이터가 어디에 가장 가까운지를 찾아서 그 레이블로 데이터를 평가하는 방식이다. 수치해석에서도 위와 같이 어느 데이터가 어디에 속하는 지 boundary를 찾는 그런 것들이 많았는데 이제야 쓰임새를 알게 되는,, 이를 위해서는 두 가지 함수가 필요한데 아래와 같다.

  1. Train 함수: 학습시키는 것으로 모든 데이터에 label을 달고 저장한다.
  2. Predict 함수: 가장 유사한 training image로 데이터를 예측한다.

이때, Distance Metric이라는 개념을 잘 이해하고 있어야 하는데, 본 강의에서도 대충 설명하고 넘어가서 이해가 안 갈 수 있다.

  1. 두 가지 거리 척도 간 차이는?
  2. L1은 좌표 시스템에 영향을 받지만 L2는 받지 않는데 왜 그런지 설명하시오.
  3. 특징 벡터의 각각 요소들이 개별적인 의미를 가졌다면 L2보다 L1을 쓰는 이유는?
  4. 추후 작성 예정

기하학적 관점: 어떤 vector의 Norm은 내적이라기 보단 해당 vector와 covector의 곱에 metric tensor를 곱해준 것인데, 이 때 metric tensor가 좌표계 or 공간이 어떻게 휘어져 있는 지에 대한 정보를 담고 있다. L1을 우선 살펴보자. L1은 내적 자체를 안 하고 그저 차이의 절댓값이니 metric에 free하다고 할 수 있다. Metric에 free하니까 그냥 변수에 대해 적분을 하면 좌표계에만 dependent하게 된다.

결국 Metirc을 고려하면 L2 Norm이랑 analogous한 개념이고, Metric이 공간이 어떻게 휘어져 있는 지 좌표계에 associate하니 좌표계가 변해도 L2 Norm은 같게 된다.

컴퓨터과학 관점: 어떤 데이터에 L1 Norm은 그냥 그 데이터 자체에서만 계산되는 값이고 L2 Norm은 그 데이터에 어떤 다른 구조(기하학 관점에서의 Metric tensor와 같은 말)를 줬을 때 나오는 값이라고 본다.

예시를 들면, 한국인의 키라는 데이터가 있고 그 키 자체에서 평균을 구하고 싶다고 하면 L1 Norm에 dependent하고 (정확한 식은 L1 Norm에 데이터 나눠준 것이지만,,) 그 키에서 분산을 알고 싶으면 L2 Norm에 dependent한 것이다. 이에 더 확장해보면 키와 나이의 correlation을 보고 싶다면 무엇에 dependent해야 할까? L2 Norm이다. 즉, 분산을 알려면 그 데이터에서 distance function인 Metric을 알아야 하는 것이다.

가령, 좌표시스템을 회전시키면 L1 distance는 변화하지만 L2 distance는 변화하지 않는다.

위에서 말했듯, 분류하고자 하는 데이터가 어디에 가장 가까운 지를 찾아야 하는데 그 기준을 설정해야 한다. 강의의 예시로는 L1 norm과 L2 norm을 예시로 들었다.

L1 norm일 때의 예시를 보면

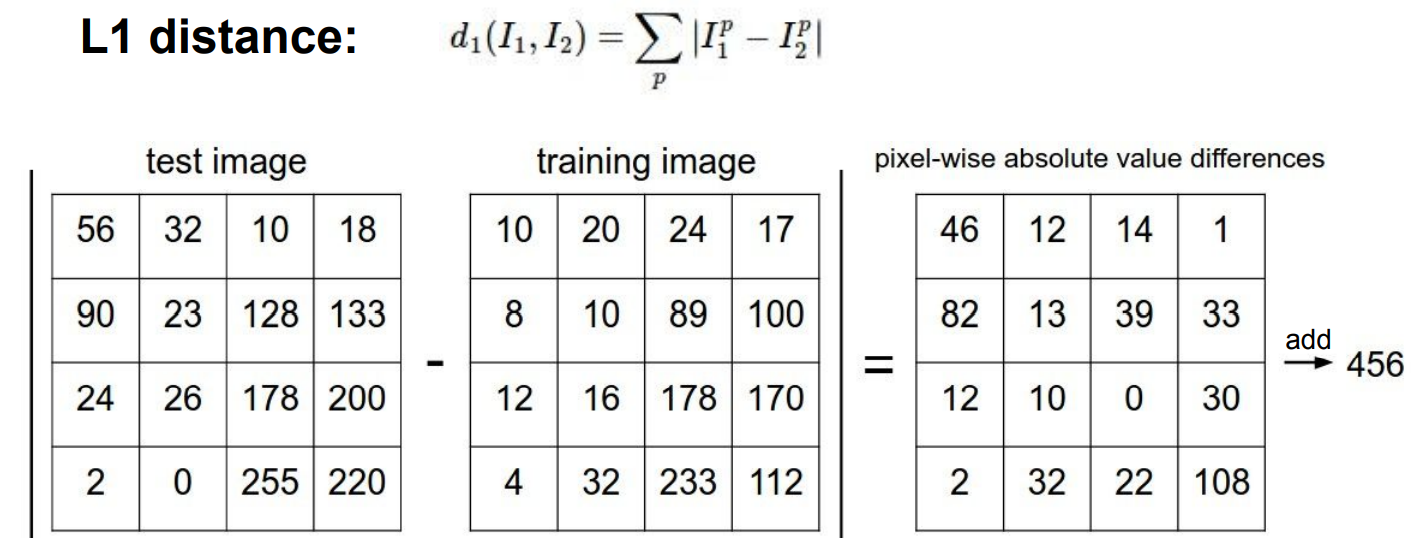
L1norm.PNG

결국 같은 자리의 픽셀값의 차이를 구하는 것이다. 이미지 분류에서 위와 같은 NN은 적합하지 않음에도 사용하는 이유는 Train시간은 O(1)이기 때문이다. 실제로 사용하지 않는 이유는 학습이 오래 걸리더라도 Test시에 빨리 동작하는 것을 원하기 때문인데 NN같은 경우 test 시에 O(n)만큼 걸린다.

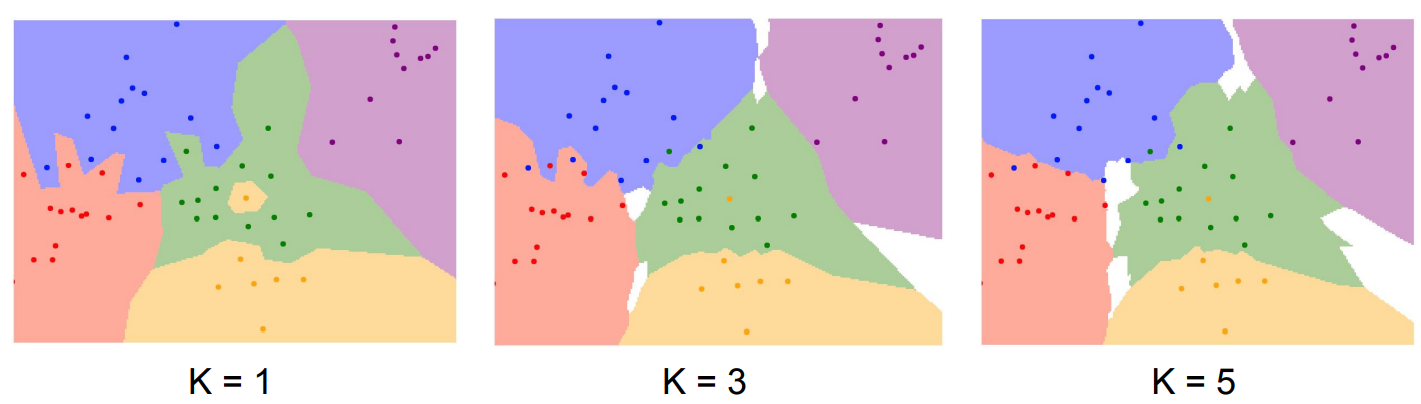knn.PNG KNN demo 갖고 놀기
K=1일 때의 결과를 얻을 수 있을 것이다. K-NN은 Nearest Neighbor만 잘 이해한다면 크게 달라질 것이 없다. 그냥 비교 집단의 원소 수가 늘어날 뿐이다. K가 커짐에 따라 점점 경계 부분이 부드러워지는 것을 확인할 수 있다.

요약하자면 K-NN 알고리즘은 가까운 이웃 K개를 찾고 자신의 label을 예측하는 것이다. 사전에 설정한 metric에 의해 기준이 바뀌고 이에 따라 결과가 바뀌는데, 이러한 변수를 hyperparameter라고 한다. 이런 값을 잘 찾아야 좋은 결과를 얻을 수 있는데, 어떻게 해야 좋은 값을 얻을 수 있을까?

K-NN Summary

Q1. 왜 K-NN은 이미지 분류에 쓰이지 않을까?

  • test time에 너무 느리다.
  • L1/L2 distance와 같은 거리 척도가 적절하지 않다. 같은 L1/L2 distance를 갖고도 완전히 다른 사진인 경우가 있다.
  • 차원의 저주로 트레이닝 데이터를 이용하여 공간을 분할하는데, 위 알고리즘이 잘 동작하려면 전체를 커버할 만큼 충분한 트레이닝 샘플이 필요하므로 차원이 늘어날 수록 그만큼 제곱이 들어가니 잘 쓰일 수 없을 수 밖에,,,

3. Setting Hyperparameters

  1. K=1인 경우(갖고 있는 dataset 전부 활용), training set에서 정확도는 높아도 해당 set에만 정확함
  2. 갖고 있는 dataset 중 일부는 test set으로 나눠서 사용: 이 또한 test set에만 잘 동작할 수 있음
  3. Train, validation, test로 테이터셋을 분리한다.

Training set으로 학습하고 validation set으로 검증하고 마지막으로 test셋으로 test를 진행하는 것이다. test셋은 마지막에 한 번 하는 것으로 즉, 새로운 정보를 얼마나 분류하는 지로 평가하는 것이다.

  1. Cross-Validation

Cross Validation

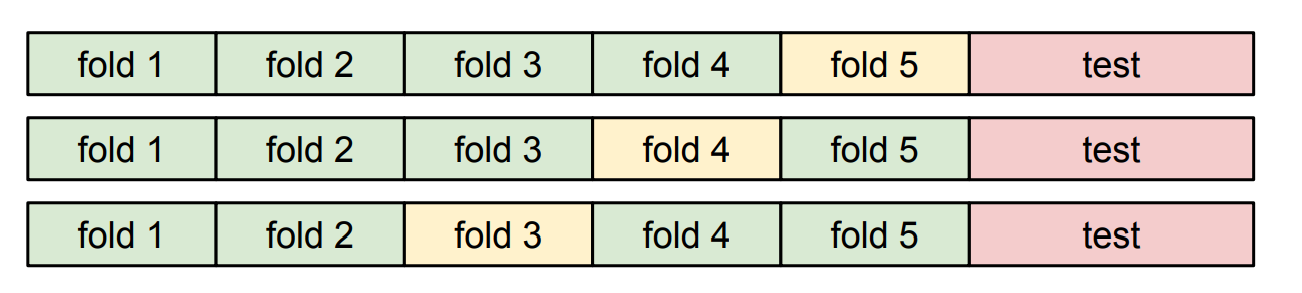
테스트 셋을 제외한 데이터를 N개로 나누고 N-1개의 fold에서 테스트를 하고 나머지 한 개에서 validation을 진행하는 방식을 반복한다.

각 하이퍼 파라미터에 대해서 이런 식으로 테스트를 하여 값을 찾는 것이다.

4. Linear Classification

Linear Classification(선형 분류)는 Nueral Network과 CNN의 기반 알고리즘으로 parametric model의 가장 기본적인 모습이다.

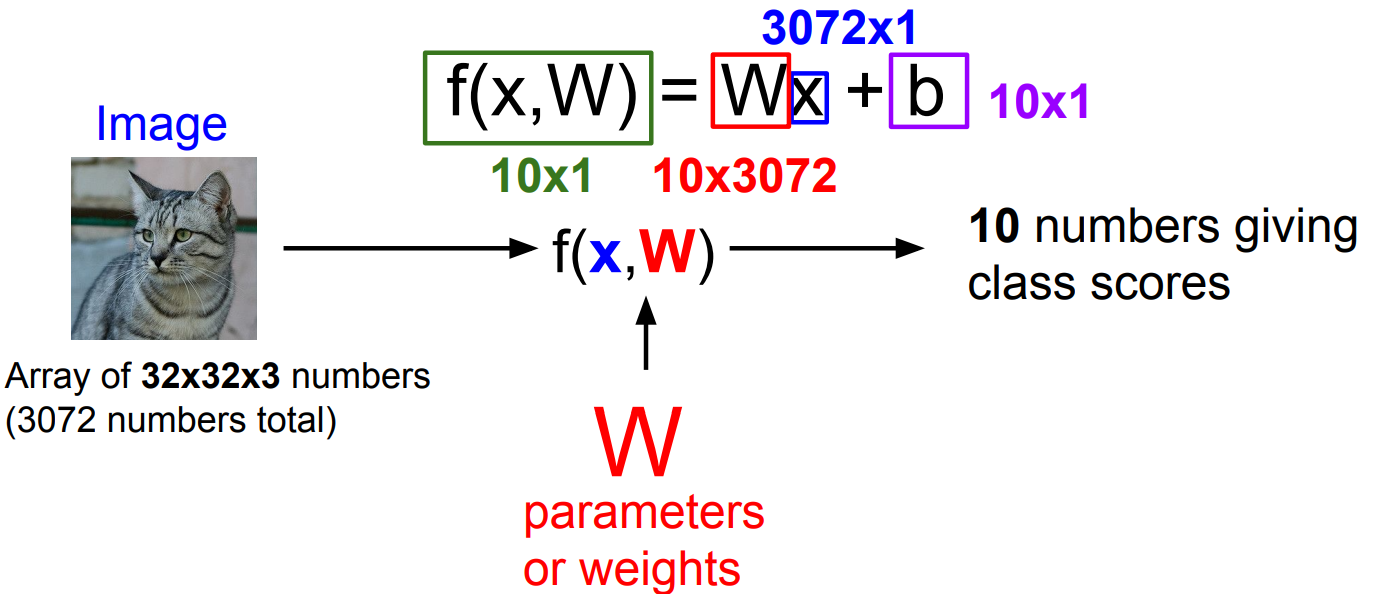
Parametric Approach

고양이 이미지를 입력한다. (32*32 사진, RGB채널 사용) 그러면 총 3072개의 수들로 이루어진 정보이다. 이를 W라는 가중치를 내적하고 b라는 bias(데이터의 편향 등)를 더 해주면 곧 함수의 output이 된다. Output인 score를 담고 있는 벡터로 유사도를 측정하는 것이다.

W라는 가중치 벡터는 어떻게 만들까? 다음 시간에…

결국, Linear classification은 템플릿 매칭과 매우 유사하다. W는 아래의 사진과 같이 각 이미지에 대한 템플릿으로 볼 수 있기 때문이다. 하지만 단일 템플릿 매칭임에 유의하자. 이를 보완한 것이 Neural Network 같은 다중 템플릿을 허용하는 모델이다. 나중에 살펴보자.

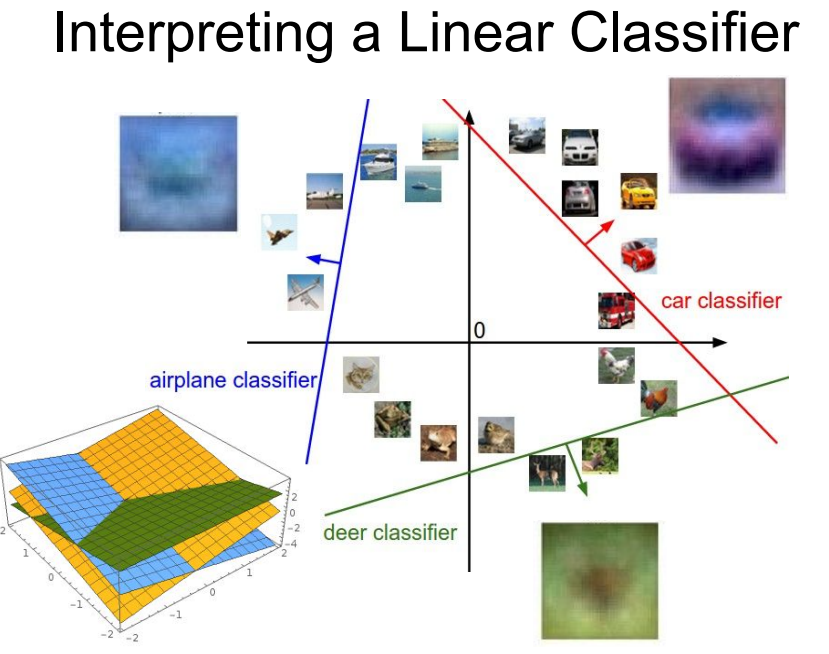
Interpreting Linear Classifier

각설하고 정리하면 위와 같이 linear한 그래프로 분류의 경계를 나타낼 수 있게 된다.

그러나, 이러한 선형 분류기를 또 다른 관점으로 해석할 수 있다. 이미지를 고차원 공간의 한 점으로 보는 것이다. 이 말을 더 쉽게 말하면 linear하지 않은 문제를 풀기 어렵다는 말과 일치한다. 예시는 아래 그림을 보자.

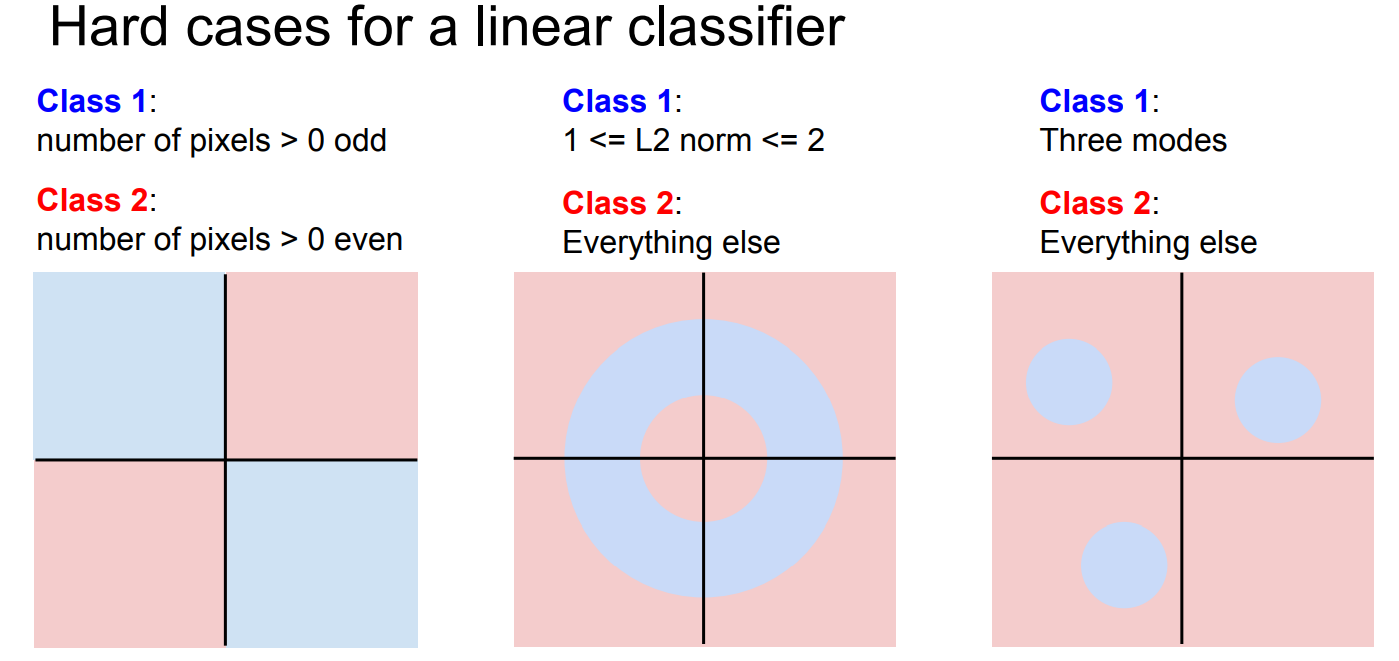
Hard cases for Linear Classifier

위와 같은 데이터를 linear하게 분류할 방법은 없다. ex) parity problem, Multimodal problem

과제 1

  • K-NN 구현하기 / Linear Classifier 구현하기(SVM, Softmax) / 2-layer Neural Network / Image features

과제 구현하러 가쉴?