[인공지능] AI - CS231n 3강 Loss Functions and Optimization

in CS Review on AI


cs231n 3강 youtube 강의 링크
cs231n 공개 강의자료
cs231n 과제 링크

CS231n 3강 - Loss Functions and Optimization

Keywords

  • Loss function
  • Multiclass SVM loss(Hinge loss)
  • Data Loss
  • L1 Regularization
  • L2 Regularization(Weight Decay)
  • Softmax Classifier(Multinomial Logistic Regression, Cross entropy loss)
  • gradient descent
  • Stochastic Gradient Descent(SGD)
  • Histogram of Oriented Gradients(HoG)
  • Bag of Words

1. Loss function

loss function(손실 함수)이란 모델의 성능을 나타내는 데 사용되는 함수로 정확히는 얼마나 나쁜지를 알려준다. 이 값이 클수록 모델의 성능이 낮음을 의미한다. 따라서, 손실 함수의 값이 작아지도록 모델을 학습해야 한다. 데이터셋이 {(xi, yi)} (i=1부터 N까지)일 때, xi가 이미지이고 yi가 레이블(x에 대한)이라면 loss는 다음과 같이 계산해볼 수 있다.
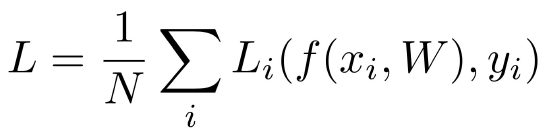
loss 계산
위 식을 풀어보면, x와 W를 통해 얻은 예측값과, 실제 정답인 y를 가지고 손실값을 구한다. 모든 데이터에 대해 반복하여 얻은 결과의 평균을 구한 것이 loss이다.

Multiclass SVM loss

(xi,yi)에 대해 얻은 결과인 score vector를 s라고 하자면 SVM loss는 다음과 같다. sj는 j번 째 클래스에 대한 점수이고, syi는 정답 class에 대한 예측 값이다.
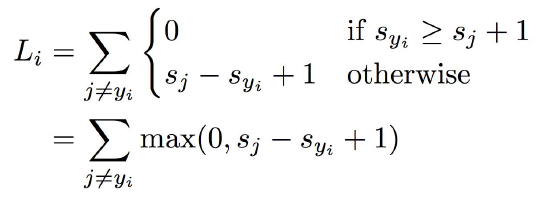
SVMloss 계산
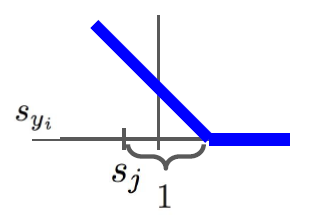
정답 class에 대한 예측값(syi)이 오답 class에 대한 예측값(sj)에 1을 더한 것보다 크면 0이 된다. 즉, 정답 class에 대한 예측을 오답 class들에 대한 예측에 비해 더 잘했다면(여기서는 그 기준이 1이며 이를 safty margin이라고 한다) loss를 0으로 간주한다는 것이다. 이를 그래프로 표현하면 아래와 같은데 마치 hinge처럼 생겨서 “hinge loss”라고도 한다.

또한 상대적으로 값을 구하기 때문에 정답 클래스가 다른 클래스보다 높냐를 중히 여긴다. 즉, 답의 점수가 어떤가는 따지지 않는다.
Hinge loss

SVM loss Example 위 사진에서 SVM loss를 구해보자. 고양이의 예시만 구해보면 아래와 같다.

max(0, 5.1 - 3.2 + 1) + max(0, -1.7 - 3.2 + 1)
= max(0, 2.9) + max(0, -3.9) = 2.9 + 0
= 2.9 (첫 번째 고양이 사진에 대한 loss)

같은 방식으로 구하면 각각 2.9, 0, 12.9이다. 이의 평균을 구하면 곧 전체 데이터셋에 대한 loss가 된다.

L = (2.9 + 0 + 12.9) / 3 = 5.27

Q1. loss값의 최솟/최댓값은?

최저는 0이며 최대는 이론상 무한이다.

Q2. 일반적으로 가중치 W를 매우 작은 값으로 초기화하는데, 모든 s는 0에 가깝다. 이때 Loss 값은?

(class 수 - 1)이다. 전부 max(0, 0-0+1)과 같은 결과를 뱉기 때문이다.

Q3. 정답 클래스 경우를 loss구할 때 포함하면?

max(0, val-val+1)과 같은 결과를 뱉기에 그렇지 않은 경우와 1만큼 차이난다. 왜 이렇게? 1보단 0이 기준 세우기 좋아서

Q4. loss가 0이 되는 W를 구했다면 이는 유일한가?

아니다!! 단순히 W의 두배만 취해도 loss는 0이다.

Regularization

loss가 0이 되도록 하는 파라미터 W는 유일하지 않은데, 이 중 가장 좋은 파라미터를 구하기 위해 Regularization을 사용한다. Regularization이란 데이터 노이즈를 제거해주고 모델에 더 적합한 피팅이 되게 쓸모없는 데이터를 걸러주는 것이라고 생각하면 된다.

가장 기초적인 방식으로는 최소제곱법이 있다. 최소제곱법은 데이터가 어떤 에러 때문에 biased되어서 나와도 신경을 안쓴다. 예시로, 특정 구간에 노이즈가 너무 큰 데이터가 있다면 참값이 특정 구간에 치우쳐진다는 말이다. 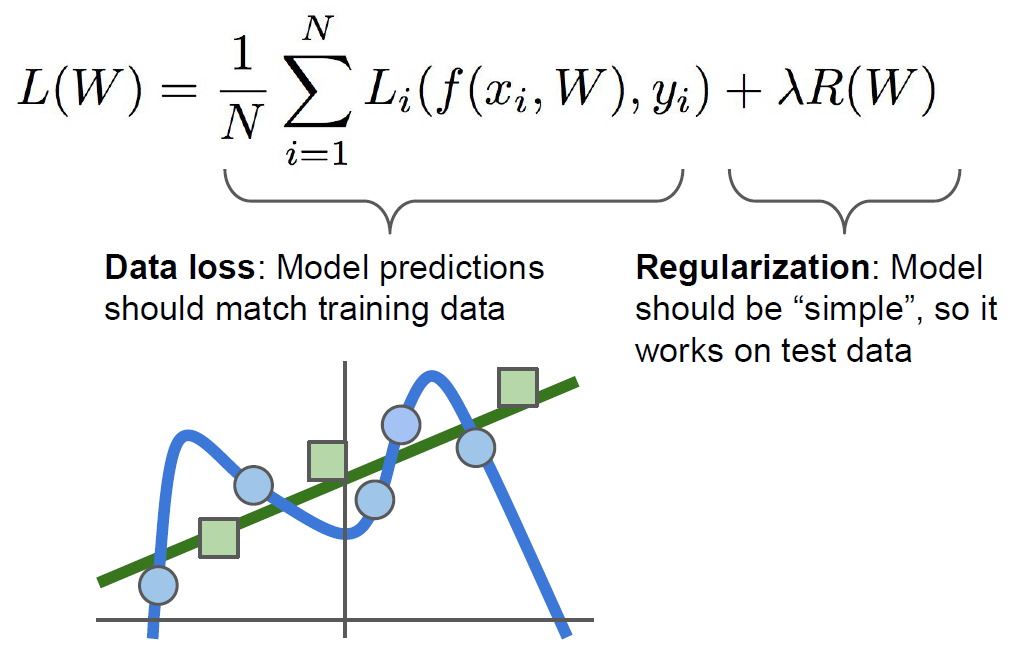Regularization
위의 그림을 보면, Data loss는 training data와 모델이 얼마나 매치되는 가를 살펴보고, Regularization은 모델을 단순화하여 test data와 얼마나 매치되는 가를 살펴본다. 감마는 하이퍼파라미터로 얼마나 정준화를 강력하게 할 것인지를 정한다.

ex) L1, L2, Elastic net(L1+L2), Max norm, Dropout, Batch normalization, stochastic depth

Softmax Classifier(Multinomial Logistic Regression, cross-entropy loss)

Softmax는 이항의 로지스틱 회귀를 다차원으로 일반화시킨 것이다. Multiclass SVM loss와 비교해보자면, Multiclass SVM loss는 예측한 점수 자체는 고려하지 않고 정답 class의 점수와의 상대적인 크기만을 중요시한다면 Softmax는 class별 확률분포를 사용해서 예측 점수 자체에 추가적인 의미를 부여, 해석한다고 볼 수 있다.
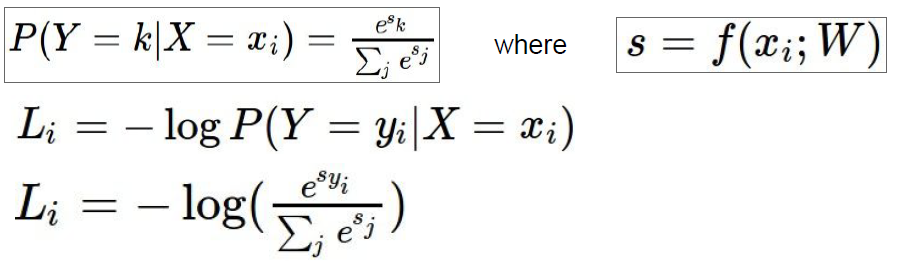
Softmax
s의 k 번째 원소는 데이터가 k 번째 class에 속할 확률을 의미하는데 데이터가 정답 class에 속할 확률은 P(Y=yi | X=xi)이고, softmax loss는 이 확률에 -log를 취한다.

exp를 취하는 이유는 확률을 구하고자 함이고 -log를 취하는 이유는 얼마나 안 좋은지를 판단해야하기 때문에, 1일 때 loss가 0이어야하고 1보다 작을 땐 loss가 0보다 커야하기 때문이다. -log함수 그래프를 그려보면 알 수 있다.
Softmax
위의 예시 데이터로 계산해보자.

cat 3.2 => e^3.2 = 24.5325...
car 5.1 => e^5.1 = 164.0219...
frog -1.7 => e^-1.7 = 0.1826...
전체 합 = 188.7371... 정답 클래스에 대해서만 구하면
cat 24.5325 / 188.7371 = 0.1299...
-log(0.1299) = 0.886.. 약 0.89만큼 구리다!!!!

Q1. Softmax의 최솟/최댓값은?

최소값은 0이며 최대값은 이론상 무한이다.

Q2. 일반적으로 가중치 W를 매우 작은 값으로 초기화하는데, 모든 s는 0에 가깝다. 이때 Loss 값은?

-log(1/c) = log(c)이다. c는 클래스의 수 이는 디버깅에 많이 이용되는데 sanity check이라고도 한다.

Q3. 예측 점수를 조금 변화시킨다면 SVM과 Softmax에서 loss는?

SVM은 상대적 차이에 관심을 두기에 큰 변화 없겠지만 softmax는 정답 클래스의 예측 점수를 확률로 변환하기에 loss에 보다 민감하다. 그러나 대폭 수정한다면 둘 다 많이 변한다.

SVM, Softmax 정리

결국 둘 다 하나의 loss를 구하는 것이며 전체적인 loss를 구하는 것은 첫 번째에 소개되어있듯 loss의 평균이며, full loss는 거기에 Regularization을 추가한 것이다. 이제 W가 어떤 기준으로 안 좋은지를 알게 되었으니 좋은 W, loss를 0으로 만드는 곳을 찾아가야 한다. 그 방법을 아래 Optimization에서 소개하겠다.

2. Optimization

최적의 loss를 구하는 방법은 간단하게 두 가지 방법이 있다.

  1. Random Search
  2. Follow the slope

1번은 말그대로 랜덤하게 접근하는 것인데 매우 안좋다. 최신의 뛰어난 알고리즘(SOTA)들은 95%에 달하는데 15.5%에 그치기 때문이다.

2번은 경사를 따라 내려가는 방법이다. 1차원이라면 미분을 통해 기울기를 알 수 있고, 다차원이라면 편미분을 통해 알 수 있다. 결과적으로, 최소의 loss를 찾아가는 것은 기울기의 반대방향으로 찾아가는 것이므로 미분한 결과에 -를 취해주면 곧 우리가 나아가야할 방향이다.

조금씩 값을 바꿔가며 기울기를 구하는 수치적인 방법이 있겠지만 이는 매우 느리므로 해석적인 방법을 사용하는 것이 좋다. 뉴턴,라이프니츠 당신은 대체… 그러나 이러한 해석적인 방법은 실수하기 쉽기 때문에 항상 수치적으로 검증해야 한다. 이를 gradient check이라고 한다.

또한 적절한 step size 즉 learning rate를 정해야 한다. 너무 큰 값을 택하면 overshooting하고 너무 작은 값을 찾으면 local minimum에 갇힐 수도, 지나치게 오래 걸린 시간이 걸릴 수도 있다.

Stochastic Gradient Descent(SGD)

N이 매우 크다면 W를 업데이트하기 위해 계산해야 하는 양도 매우 커지기 때문에 확률적으로 업데이트를 하는 방식을 사용한다. 확률적이라고 하는 이유는 전체 데이터 중 일부인 minibatch를 사용하기 때문이다. minibatch는 주로 32, 64, 128개인데 그를 바탕으로 gradient를 구하고 W를 업데이트한 후 이를 반복하여 적절한 W를 구한다.

Image features

이미지 분류에 대한 연구의 방향성은 크게 두 가지이다.

  1. feature를 추출해서 linear classifier로 분류
  2. 이미지 자체를 신경망으로 분류

1번에서 feature 추출을 color histogram, Histogram of Oriented Gradient(HoG), Bag of Words 등으로 한다. Color histogram은 color를 feature로 모든 픽셀의 color를 추출한다. HoG는 edge의 방향을 추출하고, Bag of Words는 이미지의 여러 지점(patch)를 벡터로 모아 codebook을 만든다.

2번의 경우 CNN을 사용하여 이미지 자체를 분류기에 입력해주고 그 결과값으로 학습을 한다. 이런 과정을 하려면 앞서 배운 W를 업데이트하는 기술이 필요하고 다음 강의에서 배울 Back propagation도 알아야 한다. 이건 다음 포스팅에서~~