[인공지능] AI - CS231n 4강 Backpropagation and Neural Networks

in CS Review on AI


cs231n 4강 youtube 강의 링크
cs231n 공개 강의자료
cs231n 과제 링크

CS231n 4강 - Backpropagation and Neural Networks

Keywords

  • Computational graphs
  • Backpropagation
  • Chain rule
  • local gradient / upstream gradient
  • sigmoid function
  • Jacobian matrix
  • Forword / Backword API
  • Neural Network
  • Activation Function
  • tanh
  • ReLU / Leaky ReLU
  • Maxout / ELU
  • Fully-connected layers
  • hidden layer

이전 시간에 W를 update하기 위해 loss를 최소화해야 하는데, 이를 위해 해석적인 방식을 쓰는 것이 좋다고 배웠다. 이번 강의에서는 실제로 gradient를 어떻게 구하는 지 그 방법에 대해 공부할 것이다. 이를 이해하기 위해서는 먼저 Computational graph에 대해 알아야 한다.

1. Computational graphs

Computational graphs
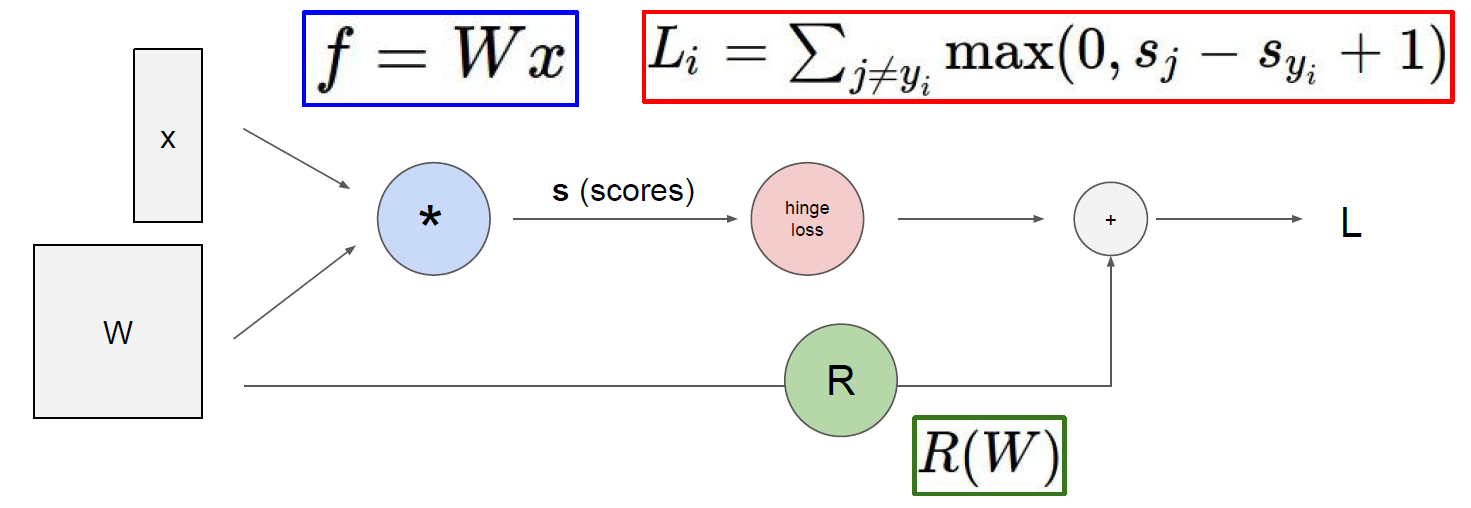
Loss를 구하는 과정을 Computational graph로 나타낸 것이 위 그림이다. input x와 가중치 W의 곱으로 s(score)를 구하고 hinge loss와 R(Regularization term)을 더해 Loss를 구한다.

Computational graph를 사용하는 주된 목적은 복잡한 연산을 나누어서 살펴볼 수 있는 부분도 있지만 Backpropagation을 통해 미분을 효율적으로 계산할 수 있다는 점이다.

복잡한 연산을 나누어서 살펴볼 수 있다는 것은 전체 계산이 얼마나 복잡하든 각 노드들 간의 문제로 분리하여 연산을 단순화할 수 있단 의미이다. 그래서 때로는 아주 자세하게 때로는 식을 압축하여 계산 그래프를 만들 수 있다. 예를 들면 *-1, exp, +1, 1/x를 sigmoid gate로 변환할 수 있다.
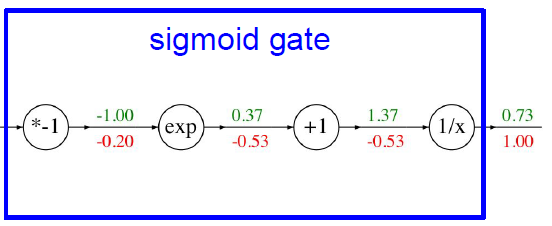
Sigmoid Gate

미분을 효율적으로 계산할 수 있게되면 어떤 노드가 결과에 어떤 영향력을 갖는 지를 알게되고 chain rule을 통해 연쇄적으로 노드들의 gradient를 계산할 수 있게 되어 loss가 최소가 되는 방향으로 업데이트할 수 있게 된다.

chain rule이란 합성 함수의 미분을 함성 함수를 구성하는 각 함수의 미분의 곱으로 나타내는 것을 말한다.

이제 Backpropagation으로 아래 예제의 local gradient들을 구해보자. local gradient는 말 그대로 해당 노드에서의 gradient를 말한다.
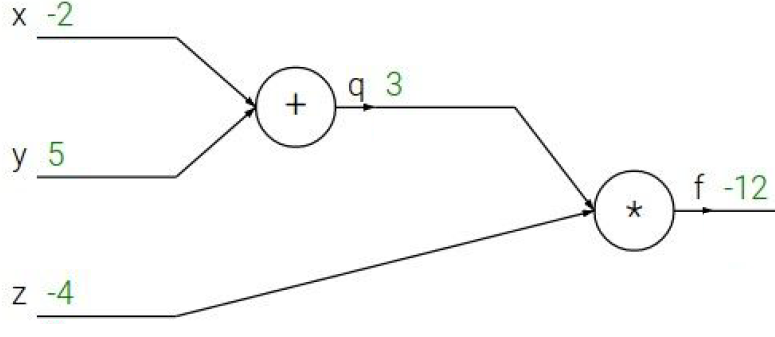
Computational graphs

x,y,z를 구하는 것이 목적인데, 결국 local gradient에 upstream gradient를 곱하는 것이다.

  1. f는 자기 자신에 대해서 미분하니까 local gradient는 1이다.
  2. f=qz이므로 f에 대한 z의 local gradient는 qz를 z에 대해 미분한 것이므로 q이다. 즉, 3이다.
  3. f에 대한 q의 local gradient는 qz를 q에 대해 미분한 것이므로 z이다. 즉, -4이다.
  4. y의 local gradient는 q의 local gradient에 q에 대한 y의 local gradient를 곱하는 것이므로(chain rule) -4 * 1이다. 즉, -4이다.
  5. x의 f에 대한 gradient는 q의 local gradient에 q에 대한 x의 local gradient를 곱하는 것이므로 -4 * 1이다. 즉, -4이다.

위 예제의 계산을 토대로 살펴보면, add gate는 gradient를 나눠주는 distributor로 볼 수 있고, mul gate는 gradient 값을 서로 바꿔주는 switcher라고 볼 수 있다. 이 밖에도 max gate는 하나의 간선에서 오는 것을 채택하기에 router라고 볼 수 있다.

만약 하나의 노드가 여러 개의 출력을 내보냈다면 이때 Backpropagation 계산은 어떻게 해야할까?

그냥 다 더 해주면 된다. 여러 개의 노드에 동일한 영향을 끼쳤기 때문이다.

2. Vectorized operations

지금까지는 scalar에 대해서 연산을 했는데 vector라면 어떨까?? 이제 jacobian matrix를 사용하여 연산해주면 된다. 사실 사용이라기보단 표현에 가깝다고 볼 수 있다. vector에서 각 변수에 대해 편미분을 하면 그게 jacobian matrix꼴이 되기 때문이다.
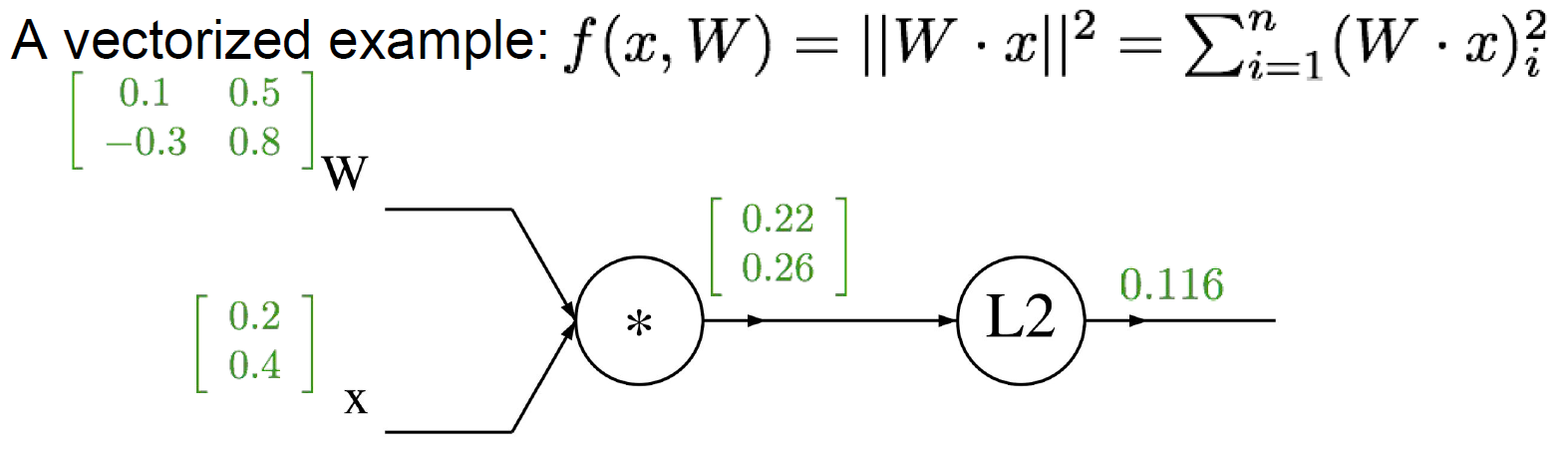
Vectorized operations

q = W · x이라 하자. f(q)는 L2 distance라서 q12+· · ·+qn2이다. f에 대해 q로 미분하면 2q라는 식을 얻을 수 있다. 앞서 배운 Backpropagation으로 식을 정리하면 다음과 같다. 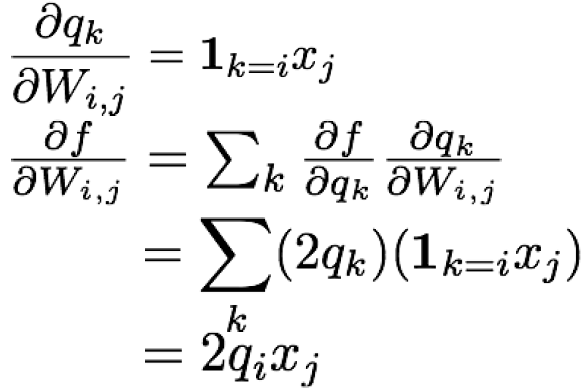Vectorized operations2

결론적으로, input인 W와 x의 gradient를 구해야 한다.
W의 f에 대한 gradient는 2q · xT이며, x의 f에 대한 gradient는 2q · WT이다. 이때, shape이 잘 맞는지 확인해야 한다. 행렬 연산은 항상 그렇듯,,

과제 1, SVM/Softmax 구현에서 forward pass API와 backword pass API를 개발해보자~~!!
cf) margins는 softmax와 같은 쓰인 classifier를 말한다.

3. Neural Networks

Neural Network는 결국 선형 분류만으로 문제가 풀리지가 않아서 생겨났다고 생각하면 된다. Linear score function으로 우리는 f = Wx를 예시로 자주 사용해왔다.

이제는 비선형 함수인 max를 사용하여 2-layer, 3-layer Neural Network로 f = W2max(0,W1x), f = W3max(0, W2max(0,W1x))를 예시로 사용하겠다.

이는 과제 2에서 구현해볼 수 있다. 벌써 과제 2..? ㅠㅠ

왜 신경망이라는 이름을 붙이게 되었을까? 우리는 뇌과학을 하는 사람이 아니니까 맞다면 다른 글을.. 간단하게 살펴보자.
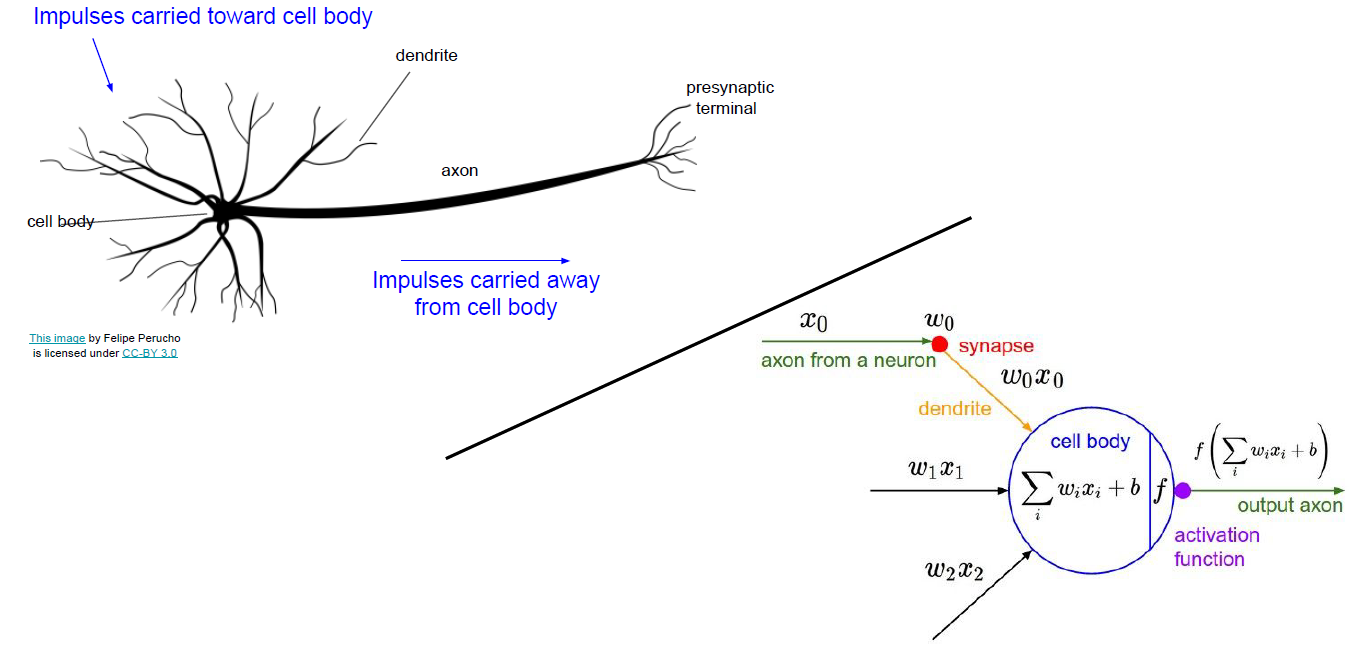
Neurons
위 그림은 신경세포인 뉴런이다. 우리가 눈여겨볼 것은 cell body, dendrite, axon, presynaptic terminal 정도이다. 이런 뉴런들이 연쇄적으로 이어져있는데, input은 다른 뉴런의 axon으로 부터 시작된다. axon과 다른 쪽 뉴런의 dendrite가 맞닿는 부분을 synapse라고 한다. 이 input이 dendrite를 거쳐 cell body로 간다.

이를 우리가 여태까지 해온 식들을 신경망에 비유해볼 수 있다. 그렇다고 해서 똑같다고 생각하면 절대 안된다!!! 비유는 비유일뿐!!

실제 우리의 뇌는 dendrite로부터 입력받은 정보들을 바탕으로 output을 다른 신경세포에 전달한다. 우리의 신경망은 얻은 정보들을 바탕으로 어떤 활성화 함수를 거쳐서 output을 얻게 된다. 그럼 어떤 뉴런이 활성화되고 어떤 건 그렇지 않을까? 어떤 기준일까?? 실제는 어떨런지..뇌과학 파이팅

이제 우리가 Activation function을 배워야할 때가 왔다. 우리는 신경망에서 이를 기준으로 뉴런을 활성화하기 때문이다!! 본 강의에서는 6 가지 함수를 소개한다.

  1. Sigmoid
  2. tanh
  3. ReLU
  4. Leaky ReLU
  5. Maxout
  6. ELU

익숙한 것도 있고, 그렇지 않은 것도 있겠지만 나중에 자세히 배울테니 추후 포스팅을 기대해주세요~~!!

신경망의 구조를 살펴보면 아래와 같다.
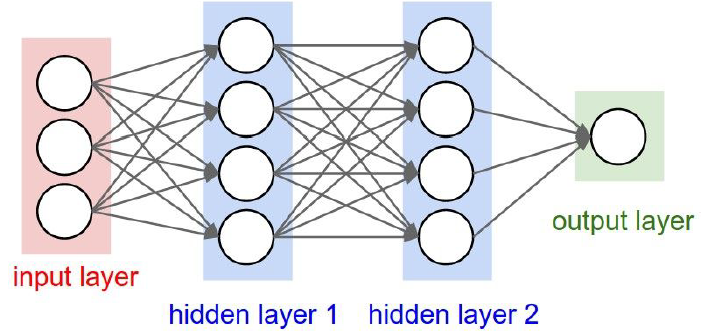
Neurons
hidden layer가 1 개일수도, 여러 개일수도 있다.그리고 그림처럼 모든 뉴런이 다음 layer의 모든 뉴런과 연결되어 있는 것을 보고 Fully-connected layers라고 한다.

다음 시간엔 드디어 CNN을 배운다. 천천히 가보자~~