[데이터 사이언스] Frequent pattern mining
in CS Review on DataScience
학습 목표
대규모 데이터베이스에서 데이터 마이닝의 테크닉 및 어플리케이션을 학습하자!!
- 데이터 마이닝의 컨셉(방대한 데이터에서 interesting한 패턴을 찾는 방법)
- 다양한 데이터 마이닝 테크닉 학습
- 데이터 마이닝 어플리케이션 이해하기
- 실세계 데이터를 데이터 마이닝을 사용해서 분석하기
- 데이터 마이닝 응용 프로그램을 개발하여 프로그래밍 능력 향상시키기
다룰 내용
- Data preprocessing
- Frequent pattern mining
- Association mining
- Data clustering
- Classification and Prediction
- Data generalization
- Outlier analysis
- Social network analysis
- Recommendation
- Other Big data issues
과제
- Frequent pattern mining: Apriori
- Classification: Decision tree
- Clustering: DBSCAN
- Recommender system
Chapter 5: Mining Frequent Patterns, Association and Correlations
- Basic concepts and a road map
- Efficient and scalable frequent itemset mining methods
- Mining various kinds of association rules
- From association mining to correlation analysis
- Constraint-based association mining
- Summary
1. Frequent pattern analysis란 무엇인가?
Frequent pattern이란 데이터셋에서 빈번하게 발생하는 어떤 패턴(아이템들의 집합, 부분열 등)을 말한다.
데이터의 내재된 특성, 규칙을 찾기 위해 생겨난 것이다. 예를 들어, “어떤 상품이 자주 같이 주문되는가?”, “컴퓨터를 사고난 다음에 살만한 물건은?”, “신약에 민감한 DNA의 종류는?”과 같은 질문들에 답을 할 수 있게 되는 것이다. 맥주와 기저귀가 자주 같이 구매한다더라..이유인즉, 남편들이 퇴근길에 아내의 심부름으로 마트에 들려 기저귀를 사면서 보상심리로 맥주도 같이 사기 때문이 아닐까..
맥주와 기저귀가 자주 같이 구매된다는 것을 알면 어떻게 활용할 수 있을까?
바로 기저귀 코너 옆에 맥주를 두는 것이다..!!
결과적으로 이런 frequent pattern들을 분석하면 Basket data analysis, cross-marketing(기저귀를 팔면서 아이 보기가 어려우십니까? 그럴땐 맥주를!!), catalog design, sale campaign analysis, web log(click stream) analysis(어떤 흐름으로 타고 들어오는가), DNA sequence analysis(병에 취약한 사람들이 공통적으로 어떤 DNA sequence를 보이더라) 등을 할 수 있게 된다.
2. 왜 Frequent pattern은 중요한가?
앞서 말한 analysis들을 할 수 있는 것만으로 frequent pattern이 중요함은 알 수 있지만 그래도 왜 중요할까?
다시 한번 말하지만, 데이터셋의 본질적 특성, 중요한 특성들을 알아낼 수 있기 때문이다. 이를 통해 데이터 마이닝 작업의 토대를 만들기도 하고, association(연관성), correlation(상관관계) 및 causality(인과관계) 등을 분석할 수 있게 된다. 또는 sub-graph처럼 순차적이고 구조적인 패턴을 얻을 수도 있다.
이뿐이랴? 시공간 멀티미디어 시계열 패턴을 분석할수도 있고, 추후에 배울 classification, cluster analysis, Semantic Data 압축 등 광범위하게 어플리케이션을 만들어낼 수도 있다.
Basic concepts: Frequent patterns & Association rules
Frequent pattern에 대해서 직관적이지만 모호하게 표현하였는데 자세히 알아보자. 먼저 이를 학습하기 위해 몇 가지 기본이 되는 컨셉을 알아야 한다.
1. Association rule을 알기 위해 아래 문장을 분석해보자.
minimum support와 minimum confidence를 만족하는 모든 Association rule(X->Y)들을 찾아라.
X는 아이템셋을 말하는데 X = {x1,…, xk}와 같이 표현된다. 말그대로 아이템의 집합을 말한다.
X->Y는 X라는 아이템셋이 있다면 Y라는 아이템셋이 발생한다라고 이해할 수 있다. 마치 “기저귀를 사면 맥주를 산다”처럼 말이다!! 앞의 예시는 아이템셋이 단일할 때의 경우고 여러 개일수도 있다. 하지만 이런 관계를 association rule이라고 부르기 위해서는 그들의 support와 confidence가 각각 minimum support와 minimum confidence보다 크거나 같아야 한다.
자 이제, Support와 confidence를 살펴보자.
Support는 아이템셋 X와 Y를 모두 포함하는 트랜잭션의 수 / 전체 트랜잭션의 수라고 할 수 있겠다. 그렇기 때문에 X와 Y를 모두 갖고 있는(X U Y) 트랜잭션의 확률이라고 표현할 수 있다. 얼핏 보면 합집합이 아니라 교집합이 맞지 않나라고 생각할 수 있지만 합집합이 맞다. 트랜잭션 관점이 아니라 아이템셋 관점이기 때문이다. 즉, X와 Y가 트랜잭션이 아니라 아이템셋이기 때문에 그 두 아이템을 모두 포함하는 것이므로 합집합이다.
Confidence는 아이템셋 X, Y를 포함하는 트랜잭션의 수 / 아이템셋 X를 포함하는 트랜잭션의 수이다. 즉, 조건부 확률이다. X를 가질 때, X와 Y를 가질 확률이다.
잘 이해가 안 갈 수 있다. 예시로 한 번 더 살펴보자. 아래의 표를 보자.
| Transaction-id | Items bought |
|---|---|
| 10 | A,B,D |
| 20 | A,C,D |
| 30 | A,D,E |
| 40 | B,E,F |
| 50 | B,C,D,E,F |
supmin이 50%이고, confmin이 50%일 때 모든 Association rule X->Y를 찾는 예시이다.
Frequent pattern은 support가 minimum support보다 같거나 큰 것을 만족하는 패턴으로 예시에는 50%이상이어야 한다.
계산해보면, frequent pattern은 {A:3, B:3, D:4, E:3, AD:3}으로 구할 수 있다.
cf) X를 보통 head라고 하고 Y를 tail이라고 하는데 association rule을 만들기 위해서 최소 두 개 이상의 아이템이 있어야 하므로 AD에 대해서만 만들 수 있다.
A와 D를 동시에 갖는 트랜잭션은 3개이고 그들 중 A를 포함하는 셋은 마찬가지로 3개이기 때문에 confidence는 100%이고, A,D를 동시에 포함하는 트랜잭션의 수는 3개이고 전체 트랜잭션의 수는 5개이기에 3/5으로 support는 60%이다.
결과적으로 association rule은 A->D(sup:60%, conf:100%), D->A(sup:60%, 75%)이다. A->D나 D->A 모두 집합에서는 같기 때문에 support는 같아야 한다.
2. 그 다음 알아야 할 것은 Closed-pattern과 Max-pattern이다.
Frequent pattern은 개념도 단순하고 찾으면 좋겠지만… Frequent pattern에 문제점이 있다. 만약 길이가 매우 긴 frequent pattern이 있다고 하자. 그 패턴의 sub-pattern 역시 frequent pattern이다. 결국 이러한 sub-patterns를 모두 고려해야 하는데, 이는 computational cost가 매우 커지는 원인이 된다.
만약 frequent pattern의 길이가 100이라면 100C1 + … + 100C100까지 모두 더한 값이 패턴의 개수가 되는데, 이는 2100-1 만큼이나 된다. 약 1.27*1030만큼이다.
그래서 frequent pattern에 redundant한 것이 너무 많으니 closed pattern과 max pattern을 구하게 된다. 아직은 잘 모르지만, 딱봐도 가짓수가 더 적은, 더 strict한 룰을 가지지 않겠는가!
아이템셋 X가 frequent하고 이와 같은 support를 갖는 super-pattern Y(X를 포함하는 Y)가 없다면 X를 closed pattern이라고 할 수 있다. 이러한 closed pattern은 lossless compression이다. 이는 곧 closed pattern만으로 frequent pattern을 만들어낼 수 있단 말이다. ex) CLOSET
아이템셋 X가 frequent하고 frequent한 super-pattern Y가 없다면 X는 max-pattern이다. 즉 더 늘릴게 없는 상황이다. ex) MaxMiner
마찬가지로 예시를 들어보자. DB에 {<a1, …, a100}, <a1, …, a50>}과 같이 저장되어 있다고 하자. 편의를 위해 두 개의 트랜잭션만을 두었다. 이때 supmin이 1이라면(support는 확률이지만 편의상 개수로 주어질 때도 있다),
Q1. 모든 frequent pattern의 가짓수는?
2100-1
Q2. Closed itemset은?
<a1, … , a100> (support: 1) , <a1, …, a50> (support: 2)
Q3. Max pattern은?
<a1, … , a100> (support: 1)
Efficient and scalable frequent itemset mining methods
Frequent pattern mining을 scalable하게 찾아내는 방법은 크게 세 가지가 있는데, 먼저 frequent pattern의 아주 중요한 특성을 소개하고자 한다. 바로 downward closure라고 부르는 property이다. 어떤 frequent한 아이템셋이 있다면, 그의 부분집합도 반드시 frequent하다는 것이다. 아주 당연한 말이다.
Scalable하게 마이닝을 해야 하는데 아래 3 가지가 대표적인 방법들이다.
- Apriori
- Frequent pattern growth(FP-growth)
- Vertical data format approach(Charm)
Scalable하다는 것은 무엇일까?
처리해야하는 데이터가 linear하게 증가할 때, 처리하는 속도가 linear하다면 이상하지 않은 상황이다. 그러나, 같은 상황에서 처리하는 속도가 exponential하게 증가한다면 좋지 않은 상황으로 scalable하지 않은 것이다. 즉, 크기나 용량이 변해도 계속 그 기능이 잘 동작할 수 있는 능력을 말한다.
1. Apriori: Frequent할 가능성이 있는 후보들을 생성하고 테스트하기
여기서 바로 앞서 배운 downward closure 명제의 대우를 사용하는데 그것이 바로 Apriori pruning principle이다. 만약 어떤 하나의 아이템셋이라도 infrequent하다면 그를 포함하는 superset은 볼 필요도 없다는 것이다. 알고리즘은 아래와 같다.
- 최초로 전체 DB를 한 번 스캔하며 1개짜리 frequent한 아이템셋을 얻는다.
- 그 아이템 셋으로부터 길이가 1 늘어난 후보를 생성한다.
- DB를 순회하면서 2번에서 생성한 후보들을 검증한다. (Minimum support 만족하는 지 확인)
- frequent set이 더 이상 나오지 않거나, candidate set이 더 이상 생성되지 않는다면 종료한다.
매우 간단한 로직이다. 혹자는 “왜 길이를 늘리면서 생성하고 매번 DB를 순회하며 테스트하지..? 그냥 전체 아이템셋을 조사하고 모든 경우의 수를 다 generate하고 DB를 1번만 scan하면서 test하면 되지 않나?” 라고 할 수 있지만 그랬다가는 앞서 말했듯 어마무시한 양의 조합을 관리하기가 힘들기 때문이다. (메인 메모리에 모두 올리는 것이 현실적으로 불가능)
위 알고리즘을 그림으로 살펴보면 아래와 같다. Supmin이 2인 것을 볼 수 있는데, 확률이 아니라 개수로 써도 무방하기 때문에 혼용하곤 한다.
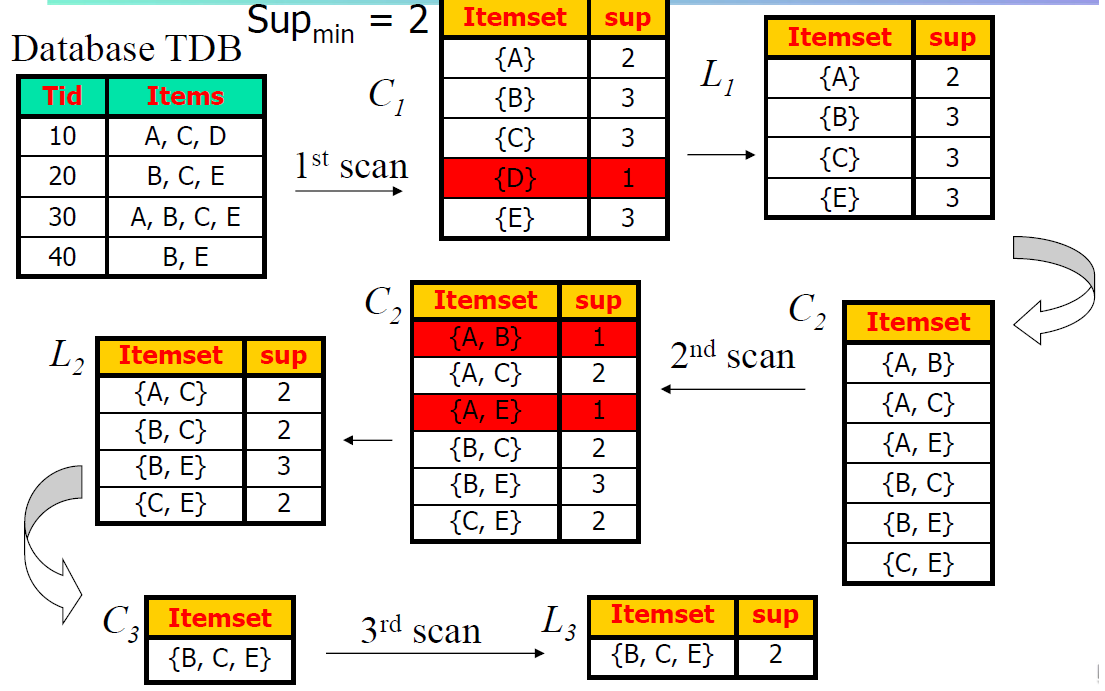
후보를 생성하는 방법은 다음과 같다. 먼저 Lk에서 self-joining을 해서 후보들을 만들어내고, pruning을 거친다. Pruning은 만들어낸 후보의 subset이 frequent하지 않다면 걸러내면 된다.
위의 그림과는 다른 예를 들면, L3={abc,abd,acd,ace,bcd}라면 self-joining을 통해 abcd와 acde를 후보로 얻을 수 있는데, acde의 subset인 ade가 L3에 존재하지 않기 때문에 frequent하지 않은 것이므로 걸러져서 C4={abcd}가 된다.
Pruning 이후엔 DB를 돌면서 support를 만족하는지 따져주며 검증하면 된다.
이러한 Apriori에는 몇 가지 문제점이 있다. 일단 길이마다 DB를 scan해야 하기 때문에 총 max length만큼 DB scan을 반복하게 되고, 후보의 수도 어마어마하다는 사실을 앞서 배웠다. 또한 support counting하는 것조차 그 workload가 상당하다.
그에 따라, 이런 문제들을 개선하는 아이디어도 생겨났다.
a. Multiple scans -> scan 횟수 줄이기
b. Huge number of candidates -> 후보 줄이기
c. Support counting -> 똑똑하게 support 계산하기
