[데이터 사이언스] Classification & Prediction (1)
in CS Review on DataScience
Chapter 6. Classification and Prediction
- What is classification & Prediction?
- Issues regarding classification and prediction
- Classification by decision tree induction
- Bayesian classification
- Rule-based classification
- Associative classification
- Lazy learners(or learning from your neighbors)
- Prediction
- Accuracy and error measures
- Ensemble methods
- Model selection
- Summary
Classification vs. Prediction
1. Classification
Categorical class labels(discrete or nominal)를 예측한다. Class label을 갖고 있는 트레이닝셋을 학습시켜 모델을 구성하고 이를 이용하여 class label이 없는 새로운 데이터를 분류한다.
Classification은 두 가지 step으로 이루어져 있다.
- Model Construction
- 목표: 모델을 사용하여 class label이 알려지지 않은 샘플을 분류
- 훈련 데이터: tuple/sample들의 집합으로 모델 생성에 사용된다.
- Tuple/Sample: <attr-1, attr-2, …, attr-n, class label>
- 모든 데이터가 class label이 있다고 가정한다.
+ 모델: 훈련 데이터로 튜플/샘플의 속성이 클래스를 결정하는 방법을 설명 - Classification rules, decision trees, networks or mathematical formulae
- Accuracy Evaluation
- 테스트 셋(트레이닝 데이터와 유사하게 클래스 라벨을 가진다)을 이용해서 모델의 정확도를 평가
- 훈련 데이터와는 독립적이지 않다면 과적합이 발생할 여지가 크다
- 모델을 통해 나온 결과와 실제 클래스 라벨을 비교하여 정확도를 계산
2. Prediction
연속적인 값을 가진 함수의 모델을 구성하고 이를 이용하여 모르거나 잃어버린 값을 예측한다. 즉, real value를 예측하는 것이다.
Classification이나 Prediction은 Credit approval(은행에서 신용 측정), target marketing(백화점같은 곳에서 고객 타겟팅), medical diagnosis, fraud detection 등에 활용된다.
Supervised vs. Unsupervised Learning
- Supervised Learning(classification): 트레이닝 셋은 class label을 포함하며 이를 학습시켜 새로운 데이터를 분류한다.
- Unsupervised Learning(clustering): 트레이닝 셋의 class label이 주어지지 않고 데이터의 클러스터를 형성한다.
Issues regarding classification and prediction
a. Data Preparation
- Data cleaing: noise나 missing value 처리
- Relevance analysis(feature selection): 관계 없거나 중복(나이와 생년)되는 attribute 제거, classification에 도움되는 attribute만 선택
- Data transformation: generalize, normalize data, 키(0~200)와 몸무게(0~100)라면 scale이 키가 더 커서 키에 의해 좌우되기에 이를 방지
b. Evaluating Classification Methods
- Accuracy
- classifier accuracy: 클래스 라벨을 얼마나 잘 분류하는가
- predictor accuracy: attribute의 값을 얼마나 정확히 예측하는가
- Speed
- 모델 생성 시간(training time)
- 실제 이용할 때 걸리는 시간(classification, prediction time)
- Robustness: 노이즈나 비어있는 값이 있더라도 모델이 잘 견뎌야 함
- Scalability: 용량이 메인 메모리를 넘는, 디스크에 있는 많은 데이터에 대한 효율성
- Interpretability: 뉴럴 네트워크는 어떻게 그러한 분류 결과가 나왔는지 이유를 잘 말해주지 못하므로 이 특성이 낮다. <-> XAI
- Decision tree size, compactness of classification rules 등
Classification by decision tree induction
1. Algorithm
- greedy algorithm으로
top-down,recursive,divide-and-conquer방식으로 decision tree를 구성한다. - 처음에 모든 트레이닝 샘플이 루트 노드에 있다.
- Attribute는 categorical 하다고 가정한다. 연속적인 값이라면 범위 나누어서 분할해서 categorize한다.
- 샘플들은 정해진 test attributes에 따라 재귀적으로 나누어진다.
재귀가 멈추는 경우는?
- 해당 노드에서 ‘모든 샘플이 같은 클래스 라벨에 속하거나’
- ‘샘플을 나눌 수 있는 Attribute가 더 이상 존재하지 않는 경우 (더 많은 수의 클래스 라벨로 분류: Majority voting)’
- ‘더 이상 샘플이 없는 경우’
2. Test Attribute Selection
그룹을 나눌 때, 좀 더 클래스 라벨이 비슷한 것끼리(more homogeneous) 잘 나누는 Attribute를 선택한다.
왜 homogeneous한 것이 좋을까?
데이터 분류에 있어서 확신을 갖을 수 있기 때문이다. 이러한 방법에는 statistical한 measure로 information gain, gain ratio, gini index 등이 있다.
Attribute Selection Measure
우리는 앞서 homogeneous한 것이 더 좋은 것을 배웠는데 이를 어떻게 측정할 수 있을까? 우리는 3 가지 방법들을 배울 것이다.
1. Information Gain
- 가장 높은 information gain을 얻는 test attribute를 선택!!
- 엔트로피(expected information)
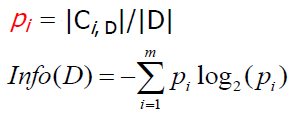
pi는 전체 데이터 중 클래스 i에 해당하는 데이터의 수이다.
모든 class label의 value마다 전체 튜플 중 그 class label의 확률(pi)을 대입하여 값을 구한다. 위 식에서는 class label의 value의 종류가 m개인 경우이다.
더 다양할수록(more heterogeneous) 큰 엔트로피(expected information) 값을 갖는다.
엔트로피는 다른 말로 얼마나 복잡한가, 얼마나 다양한가, 얼마나 놀라운가 등으로 바꾸어 생각해볼 수 있다. 정의가 헷갈린다면 위의 기준들을 떠올려보자.
Information gain 공식을 살펴보자. 아래 식은 A라는 attribute를 기준으로 split했을 때의 information gain을 구하는 공식이다.
Gain(A) = Info(D) - InfoA(D)
Information gain은 분기 이전의 엔트로피에서 분기 이후의 엔트로피를 뺀 값이다. 분기 전의 엔트로피는 앞서 구했고, 분기 후의 값을 구해보자.
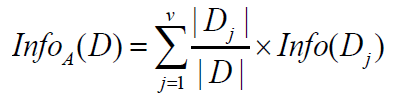
A라는 Attribute로 D를 v개(attribute value의 종류가 v 가지)의 partition으로 나누었다고 한다면 sum은 j=1부터 v까지의 weighted average한 entropy의 합이다.
이제 각 성분이 무엇이고 어떻게 계산되는 지를 알게 되었다. 그렇게 구한 information gain이 큰 값을 택해야 할까 작은 값을 택해야 할까?
정답은 큰 값을 택해야 한다. 왜 그럴까?
엔트로피가 크면 그만큼 여러 값이 섞여 있는 복잡한 상태인데, 다음 분기의 상태가 덜 섞인, 즉 잘 분류된 상황이어야 좋지 않겠는가
결과적으로 분기 후의 엔트로피가 제일 작은 값을 택한 것이 information gain을 제일 크게 만드는 것이 된다. 즉, 얻은 정보량이 제일 크다고 해석하면 된다.
만약 attribute가 categorical하지 않고 연속적인 값을 갖는다면 어떻게 분기를 나눠야할까?
Attribute 값을 이산적으로 변환하고 split point를 결정해야 한다.
Attribute 값에 따라 증가하는 순서대로 정렬한다. 두 value 사이의 중간 값들을 split point로 볼 수 있다. 아래 그림을 보면 이해하기 쉽다.
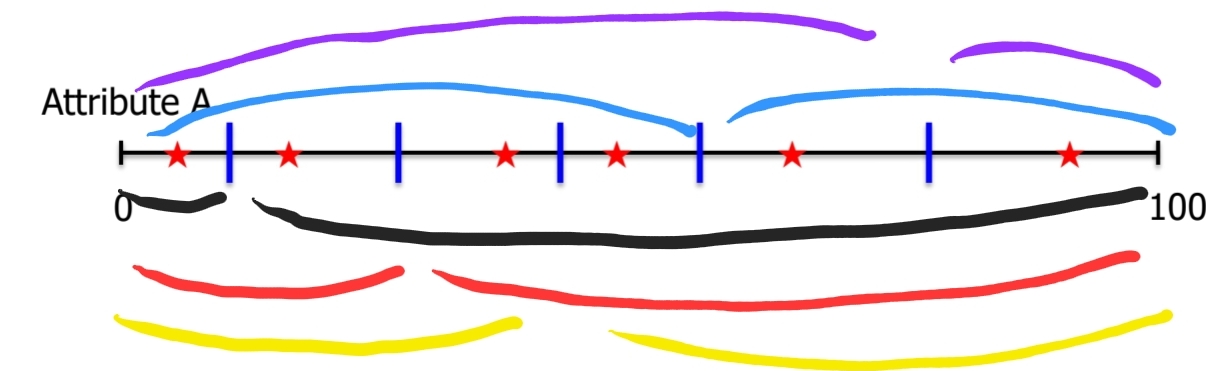
위와 같이 연속적인 값들의 중간 지점들이 곧 split point이다. 각 split point에서의 entropy를 계산해야 한다. 위의 그림에서는 5 개의 split point가 있으므로 5 개의 entropy 값을 얻을 텐데 이 중 제일 적은 값을 갖는 point가 바로 best split point가 된다. 즉, maximum information gain을 얻는 point이다.
위 그림은 binary partition을 전제로 계산하고 있는데, n-ary partition일 경우 또한 생각해볼 수 있다. 그러나, combinatorial number of partition만큼 엔트로피를 계산하기 때문에 데이터가 많다면 수많은 엔트로피 연산이 필요해서 성능에 심각한 문제가 발생한다.
Information gain은 마냥 좋은 measure가 아니다. 이는 값이 많은 attribute로 편향되어 있다. 무슨 말이냐면 A, B 두 개의 attribute가 있다고 하자. A는 5 개의 값을 갖고 B는 2 개의 값을 갖는다면 A가 B보다 큰 information gain을 얻을 것이다.
이러한 문제를 해결하고자 gain ratio라는 방법이 제시되었다.
2. Gain Ratio(C4.5에 사용됨)
Gain Ratio는 Information gain의 attribute value의 수가 많을수록 커지는 경향을 해결하고자 한다. 아래는 gain ratio의 공식이다.
GainRatio(A) = Gain(A) / SplitInfoA(D)
Gain(A)는 앞서 information gain에서 다룬 값으로 Info(D)-InfoA(D)이다.
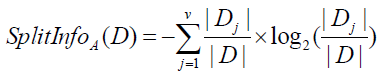
공식을 보면 어딘가 익숙하다. Normalization이 떠오르지 않는가? Gain ratio는 information gain에 대해 normalization을 해준 결과이다. Normalization으로 input data의 편향을 해소해준 것이다. Gain(A)가 쓸데없이 커진다면, 분모에 똑같이 커지는 값으로 나눠준다면 조금은 해소된다!!
결과적으로 information gain과 마찬가지로 gain Ratio가 가장 큰 attribute가 선정된다.
이 역시도 만능이 아니다. 불균형이 심한 attribute(더 작은 쪽)를 상대적으로 선택하기 쉬워진다.
3. Gini Index(CART에 사용됨)
gini(D) = 1-sum(pj2)
pj: class label에 대한 확률
N개의 class label에 대하여 gini index를 계산하는 공식이 바로 위 식이다.
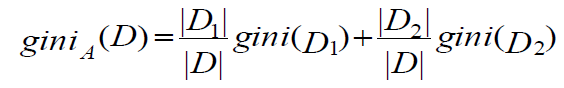
위 식에서 attribute A는 binary partition을 가정한다. 즉, 하나의 attribute가 여러 개의 value를 지닌다면 binary split을 해야 한다. 그렇게 해서 binary로 나눈 attribute set들에 대해 각각 gini index를 구하고 그 값의 weighted average를 구해서 각각 더해주면 된다.
Gini index도 마찬가지로 변화량이 제일 큰 것을 선택한다.
Reduction in impurity: delta gini(A) = gini(D)-giniA(D)
결과적으로 가장 reduction in impurity(heterogeneity)가 큰 attribute를 선택한다. 결국 가장 작은 giniA(D)값을 선택해야 한다.(= delta gini(A)값이 가장 큰 경우)
Gini index는 binary partition을 가정하므로 split point 중에서 가장 giniA(D)가 작은 값의 지점을 고려해야 한다.
예시로, 어떤 attribute의 값이 low, medium, high가 있으면 low, medium/high로 나누거나, low/medium,high, low,high/medium로 나눈다.
그렇기 때문에 partition이 균등하게 이루어지는 attribute를 선호한다.
이 방법 역시 단점이 있다. 클래스 수가 많을수록 계산하기 어려워진다는 점이다.
Overfitting
Overfitting이란 무엇인가? 훈련 데이터셋을 학습시키는 과정에서 발생하는 현상이다. 과하게 훈련 데이터에 적합한 상황이다.
오늘 우리가 배운 decision tree에서의 overfitting은 극단적인 경우 모든 튜플이 각각 하나의 브랜치를 갖고 있는 경우이다.
결과적으로, 너무 많은 브랜치가 있다보니 noise나 outlier 때문에 이상한 결과를 낼 수 있고, 새로운 데이터에 대해서 낮은 정확도를 보인다.
Decision tree에서 이러한 overfitting을 어떻게 피해갈 수 있을까?
a. Prepruning
기본적으로 tree 생성, 연장을 조기에 종료하는 방식이다.
Goodness measure가 미리 정해둔 값(threshold)으로 떨어지면 더 이상 브랜치를 생성하지 않는 방법이다. 예를 들어, information gain의 정도가 미미하다면 트리의 성장을 멈추는 것이다.
그러나, 적절한 threshold를 정하기가 어려운 한계가 있다.
b. Postpruning
기본적으로 만들어진 decision tree(“fully grown tree”)에서 브랜치를 지우는 작업이다.
Pruned tree들을 여러 개 만든 후 훈련 데이터셋이 아닌 데이터셋 아마도 evaluation set 으로 정확도가 가장 높은 tree를 고른다.
Classification in large databases
Classification은 통계학자 및 기계 학습 연구자가 광범위하게 연구하는 고전적인 문제이다. Unknown data를 정확하게 분류하는 것이 목적인데 적절한 속도로 수백만 개의 예제와 수백 개의 속성을 가진 데이터셋을 분류하는 scalability가 중요하다.
그래서 우리는 앞서 배운 decision tree induction을 데이터 마이닝에 사용한다. Decision tree는 다음과 같은 장점들을 지닌다.
- 상대적으로 학습 속도가 다른 classification method들에 비해 빠르다.
- 간단하고 쉽게 이해할 수 있는 classification rule로 변환 가능하다.
cf) Rule의 개수는 root에서 leaf까지 경로의 개수이며, 여러 노드를 거쳐서 분류할 때 각각 attribute와 그 값의 쌍은 교집합으로 연결된다. 튜플은 단 하나의 path만 지나쳐서 서로 배타적이고 exhaustive하다(Rule conflict가 발생하지 않는다, 무조건 분류함). - DB(disk, ssd)에 있는 데이터를 sql query로 접근할 수 있다.
- 다른 classification 방법들에 비해 정확도가 썩 나쁘지 않다.
