[데이터 사이언스] Classification & Prediction (2)
in CS Review on DataScience
Chapter 6. Classification and Prediction
- Bayesian classification
- Rule-based classification
- Associative classification
Bayesian classification: why?
왜 bayesian classifier를 사용할까? 크게 3 가지 이유가 있다.
1. Statistical classifier
통계적인 classifier이기 때문이다. 베이즈 정리를 기반으로 하며 확률론적 예측으로 분류한다.
2. Performance
Simple naive bayesian classifier는 decision tree나 neural network에 뒤떨어지지 않는 성능을 가진다.
3. Incremental
기존 데이터에 추가적인 데이터를 학습시키기 용이하다. 즉, 데이터를 추가한다고 해서 전체 데이터를 다시 학습시킬 필요가 없다. 그저 확률 셈(확률 테이블 수정)을 다시해서 줄이거나 높이기만 하면 되기 때문이다.
Bayesian Theorem: Basics
베이즈 정리란 무엇인가? 이를 알기 위해선 간단하게 확률과 관련한 표현들을 먼저 알아야 한다.
- X를 class label이 알려져 있지 않은 데이터 샘플(evidence)이라고 하자.
- H는 ‘X가 class C에 속한다’라는 가설이라고 하자.
이 때, P(H|X)는 X가 주어졌을 때 H를 만족할 확률이다. 이 값이 가장 높은 클래스로 분류한다.
P(H)는 prior probability라고 하며, X와 독립적인 initial probability를 말한다. X가 주어지기 전의 가설을 만족할 확률로, X가 age나 income(다른 attribute)과 상관없이 컴퓨터를 살 확률(class label)을 예로 들 수 있다.
P(X)는 X라는 샘플 데이터가 전체 데이터에서 발생할 확률을 말한다.
P(X|H)는 posteriori probability라고 하며, H라는 가설을 만족할 때, X라는 데이터를 가질 확률을 말한다. X가 컴퓨터를 산다고 할 때, X의 나이가 31~40이고 연봉은 medium일 확률을 예로 들 수 있다.조건부 확률(Conditional probability)
P(X|H)=P(X intersection H) / P(H)P(H|X)=P(X intersection H) / P(X)- P(X intersection H) =
P(H|X)* P(X) =P(X|H)* P(H)
이제 베이즈 정리를 위한 확률적인 표현은 모두 배웠다. 베이즈 정리는 다음과 같다.
P(H|X) = P(X|H) * P(H) / P(X)
X 데이터(training)와 사후 확률(posteriori probability) P(X|H)가 주어졌을 때, P(H|X)를 구할 수 있다.
이는 곧 우도와 같다.
Likelihood(우도) = posteriori(사후확률) * prior(사전확률) / evidence
모든 클래스 중에서 P(Ci|X)가 가장 큰 값을 가지는 클래스로 분류한다.
실질적으로 많은 데이터에 대해서 확률을 다 알아야 하니까 computational cost가 많이 든다. 이를 어떻게 해결할 수 있을까?
Naive Bayesian Classifier
D를 튜플 및 관련 클래스 레이블의 training set이라고 하고, 각 튜플은 n차원의 attribute를 갖는다.
X = (x1, x2, …, xn)
M개의 클래스들이 있다고 가정하자. Classification은 곧 최대 사후 확률 얻는 것이기에 P(Ci|X) = P(X|Ci)*P(Ci) / P(X)를 튜플마다 구해주어야 하는데, 결국 모두 같은 P(X)를 사용하기에 분자만을 계산하고 이 값이 최대가 되게끔 하는 값을 찾으면 된다.
그러나 이 또한, computational cost가 크기 때문에 attribute가 다 독립적이라고 가정하고 계산 해준다.
정리하면, P(X|Ci) = P(x1|Ci) * P(x2|Ci) * … * P(xn|Ci)
로 계산하여 computation cost를 굉장히 많이 줄일 수 있다. Class distribution만을 세기 때문이다. 앞서 incremental하다고 했었는데, 새로운 것이 들어오면 계산하고 곱해주면 끝이다.
만약 attribute Ak가 categorical한 경우, P(Xk|Ci)는 (Attribute 값이 Xk인 튜플의 수)/(Ci에 속하는 튜플 수)와 같다.
혹은 attribute가 continuous-valued인 경우, 가우시안 분포를 따른다고 가정하고 평균과 표준편차 값을 계산하고 P(Xk|Ci)를 계산한다.
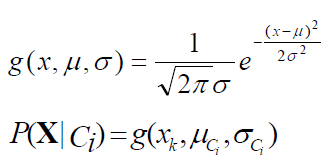
cf) 평균 = class Ci의 평균, 표준편차 = class Ci의 표준편차
하지만 독립적이라고 생각하고 곱셈으로 확률을 구해주었는데, 중간에 확률이 0인 값이 하나라도 섞여 있다면 다른 값들과는 관계 없이 0이 되어 버린다. 그렇기 때문에 Naive bayesian prediction은 조건부 확률이 0이 되지 않는 것을 전제로 한다. 이를 어떻게 해결할 수 있을까?
가장 간단하게 해결하는 방법은 Laplacian correction(or Laplacian estimator)의 아이디어를 차용하는 것이다.
모든 attribute의 값마다 1을 더해준다. 해서 어떤 경우에도 확률이 0인 경우가 나오지 않게끔 전처리를 해주는 것이다.
결과적으로 분모에는 attribute의 개수만큼 더해주고, 분자에는 1을 더해주면 되고 전체적인 확률은 크게 변하지 않는다.
이러한 Naive Bayesian prediction의 장단점은 무엇일까?
장점
- 구현하기 쉽고 데이터가 늘어나면 그저 기존 모델에 새로운 데이터 추가하면 된다.
- 대다수 상황에 좋은 결과를 얻을 수 있다.
단점
- Attribute끼리 독립적이라는 가정을 기반으로 하기에 이 가정이 맞지 않을 경우 정확도 손실이 생긴다.
- 실제로 독립적이지 않은 attribute가 존재한다. 예를 들어, 환자의 나이가 많을수록 각종 병에 취약하듯이 말이다.
이러한 attribute간의 의존성을 어떻게 해결할 수 있을까?
Bayesian Belief Networks
Rule-based classification
IF-THEN Rules를 사용해서 분류를 할 수 있다. Knowledge를 IF-THEN rule을 사용해서 표현한다. IF 부분은 rule antecedent/precondition이라고 하고, Then 부분은 rule consequent라고 한다.
Rule R에 대한 평가 기준으로는 coverage와 accuracy가 있다.
Coverage는 rule R로 분류가 가능한 것의 확률이다. 즉, ncovers / |D| 이다.
Accuracy는 분류가 가능한 것들 중에서 올바르게 분류될 확률로 ncorrect / ncovers이다.
만약 2 개 이상의 룰에 해당된다면 conflict resolution이 필요하다.
- Size ordering: Rule의 antecedent에서 테스트하는 attribute의 개수가 가장 많은 즉, 가장 tough한 rule을 고른다.
- Class-based ordering: Rule의 consequent를 보고 판단한다. Misclassification cost per class(각 class의 정확성을 보고, 더 정확성이 높은 rule의 consequent를 따른다.) 혹은 decreasing order of prevalence(frequency, class의 개수 순으로 내림차순하여 개수가 많은 것을 따른다)가 있다.
- Rule-based ordering(decision list): Domain expert가 사전에 기준을 정해서 우선순위를 정한다.
Associative Classification
Association rule들은 classification을 하기 위해 생성되고 분석된다. Frequent pattern(conjunctions of attribute-value pairs)들과 class label 사이의 association이 strong한 것을 찾는다.
P1 ^ P2 ^ … ^ Pi -> “Aclass=C”(conf, sup)
왜 효과적일까?
많은 attribute 중에서 가장 높은 association을 가진 것을 탐색한다. Decision tree와 비교해보면 decision tree는 한 번에 하나의 attribute만 고려하고 rule이 exclusive하지만 associative classification은 rule이 exclusive하지 않아서 하나 이상의 rule에 해당되고 그에 따라 일부 제약 조건을 극복할 수 있다.
또한 많은 연구에서 associative classification은 C4.5와 같은 전통적인 분류 방법보다 더 정확하다고 알려져 있다.
정확도는 높지만, conf와 sup의 threshold를 높이면 cover가 되지 않는 rule이 많이 나올 수 있다. 또한 생성된 rule들은 disjoint하지 않을 수도 있다.
