[데이터 사이언스] Classification & Prediction (3)

Chapter 6. Classification and Prediction

Lazy learners(or learning from your neighbors)
Prediction
Accuracy and error measures
Ensemble methods
Model selection
Summary

Lazy vs. Eager learning

1. Eager learning

앞서 다뤄왔던 방법들이 전부 eager learning에 해당한다. 훈련 데이터셋이 주어지고, 새로운 테스트 튜플을 받기 전에 분류 모델을 만들고 테스트 셋이 오면 바로 모델에 넣어 분류를 하는 방식이다. 그렇기 때문에 테스트 샘플들은 분류가 이뤄질뿐 모델에 어떠한 영향을 주지 않는다.

결과적으로 eager method는 전체 데이터를 다 다룰 수 있는 하나의 모델(hypothesis)을 만들어야 한다.

2. Lazy learning

다른 말로 instance-based learning, lazy evaluation이라고도 한다. 훈련 데이터셋을 그냥 저장해두고 테스트 튜플이 주어질 때까지 기다린다. 그렇기에 학습할 때는 시간이 적게 걸리지만 예측할 때 더 많이 걸린다.

Lazy method는 많은 eager method와 달리 단일 가설을 사용하지 않고 많은 local function들이 합쳐진 복잡한 hypothesis space를 사용한다.

예시로는 K-nearest neighbor approach가 있다. KNN 알고리즘으로도 익숙한 그것이다.

K-Nearest Neighbor Algorithm

모든 instance들(n 개의 attribute 소유)은 n차원 공간에 대응된다. 거리는 그 공간에서 정의된다. 그래서 테스트 샘플이 주어지면 거리가 가장 가까운 k개의 샘플을 가져오고 그 중에서 다수의 class label를 따라간다.

KNN

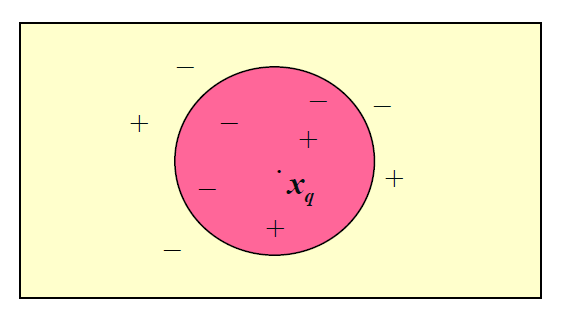
위 그림에서 k는 5이고 X_q의 class label은 -가 될 것이다.

이외에도, weighted voting을 할 수도 있다. 거리의 역수를 weight으로 해서 weighted count를 해서 구할 수 있다. 그래서 위의 예제에서 보면, 다수는 -지만 weighted voting을 통해서 class label은 +로 선택될 수 있다.

Dist function을 잘 선정하고, 필요한 attribute만으로 분류를 할 때 잘 작동한다.

What is Prediction?

Numerical prediction은 classification과 비슷하다. 모델을 만들고 그 모델로 input의 continuous value를 예측하는 점에서 말이다. 그러나 classification하고는 다르다.

Classification은 categorical class label을 예측하는 반면 prediction은 continuous-valued function 모델을 이용하여 continuous space의 값을 예측하기 때문이다.

Prediction의 주요 방법 중 하나는 regression이다. Regression은 한 개 이상의 predictor variables(예측 변수, 독립 변수 등)와 response variable(종속 변수) 사이의 관계를 모델링하는 것이다.

Regression analysis

1. Linear regression 1개의 독립변수 x와 종속변수 y로 선형함수를 이루는 선형 회귀이다.

y = w₀ + w₁x

트레이닝 데이터로 가장 잘 맞는 직선을 찾는 것이다. 즉 x의 계수와 w₀을 찾아야 한다. 찾는 방법으로는 least square method가 있다. 최소제곱법인데 말 그대로 실제값과 함수값의 차이의 제곱이 최소가 되도록 하는 w₀와 w₁을 찾으면 된다.

LSM

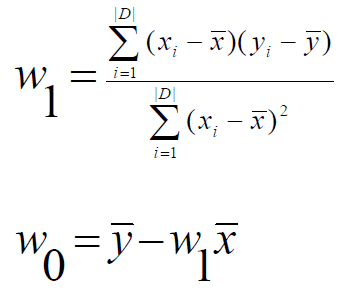
cf) 변수 위의 바는 평균을 말한다.

2. Multiple linear regression

Linear regression은 독립변수가 하나였지만 이제는 두 개 이상인 경우이다.

X = <x1, x2, x3, …, xn> : Predictor variables

만약 2차원의 data라면 함수는 아래와 같다.

y = w₀ + w₁x₁ + w₂x₂

이 역시 parameter들을 구해야 하는데, least square method를 확장한 방법이나 SAS, S-Plus와 같은 툴로 구할 수 있다.

3. Non-linear regression

항상 linear하게 대처하는 것은 아니다. 대체로 더 잘 맞는 nonlinear하게 해결하는 모델들도 있다. 어떤 nonlinear 모델들은 다항 함수로 나타낼 수 있다. 다항함수 regression model은 linear regression model로 바꿀 수 있다. 예를 들면,

y = w₀ + w₁x₁ + w₂x² + w₃x³

위와 같은 nonlinear한 식의 경우 x제곱과 x세제곱을 각각 x₂, x₃으로 치환해서 풀 수 있다.

다른 regression 방법들
- Generalized linear model
- Poisson regression
- Log-linear models
- Regression trees

Accuracy and error measure

1. Classifier and error measure

Confusion matrix

	C1(classified: positive)	C2(classified: negative)
C1(ground truth: True)	True positive	False negative
C2(ground truth: False)	False positive	True negative

일반적으로 진단해야 하는 질병, 감지해야 하는 사기행각 등을 positive로 둔다. 진양성, 위양성, 진음성, 위음성 헷갈릴 수 있는 데 아래와 같이 생각하면 안 헷갈릴 수 있다.

True/False는 실제 class label과 분류한 결과의 일치 여부를 말하고,
Positive/Negative는 분류한 결과가 양성인지 음성인지를 말한다.

다시 말해서, True positive라면 분류기의 결과가 양성이고 그것의 ground-truth도 양성인 경우를 말한다.

아래와 같은 예시를 살펴보자.

classes	buy_computer = yes	buy_computer = no	total	recognition(%)
buy_computer = yes	6954	46	7000	99.34
buy_computer = no	412	2588	3000	86.27
total	7366	2634	10000	95.42

분류기 M의 accuracy를 acc(M)이라고 하자. acc(M)의 값은?

(6954+2588)/10000 = 0.9542

분류기 M의 Error rate(misclassification rate)는?

1 - acc(M) = 1 - 0.9542 = 0.0458

위와 같이 진양성, 진음성을 이용한 accuracy 측정 방법도 있지만 다른 방법도 있다. 예를 들어 암을 진단하는 상황을 생각해보자. 수치는 위의 표와 동일한 표를 생각해보자.

Sensitivity(민감도) = t-pos / pos (= recall) // True positive recognition rate, 질병이 있는 사람을 얼마나 잘 찾아내는가
Specificity(특이도) = t-neg / neg // True negative recognition rate, 정상을 얼마나 잘 찾아내는가
Precision(정밀도) = t-pos / (t-pos + f-pos) // 양성이라고 판단한 것 중에 진짜 양성의 비율
Accuracy(정확도) = sensitivity * pos/(pos+neg) + specificity * neg/(pos+neg)
= t-pos / (pos+neg) + t-neg/(pos+neg) = (t-pos+t-neg)/(pos+neg)

위와 같은 방식으로 accuracy를 계산할 수 있다. Sensitivity(recall, 재현율)는 암 걸린 사람들 중에 암에 실제로 걸렸다고 진단한 사람들의 비율이고, specificity는 암에 걸리지 않은 사람들 중에 암에 걸리지 않았다고 진단한 사람들의 비율이며 precision은 암에 걸렸다고 진단한 사람들 중에 진짜 암에 걸린 사람들의 비율이다.

결과적으로 암환자에게 암이 아니라고 예측한 경우는 치명적이다. = 그렇기에 recall이 높아야 한다!!

스팸 메일이라고 예측했는데 그 중에 정상 메일이 있는 경우는 치명적이다. = 그렇기에 precision이 높아야 한다!!

2. Predictor Error Measures

a. Measure predictor accuracy

예측값이 실제값(ground truth)보다 얼마나 멀리 떨어져 있는가!

b. Loss function

실제값과 예측된 값의 차이(=에러)를 측정한다.
- Absolute error: |yi-yi’| = 차이 보존하고 싶을 때
- Squared error: (yi-yi’)² = 하나라도 크게 틀리면 페널티를 많이 주고 싶을 때

c. Test error(generalization error)

테스트셋의 loss의 평균을 말한다.
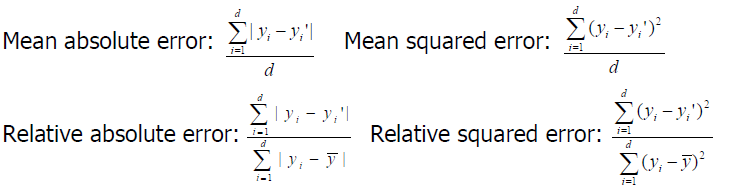
Mean squared error는 아웃라이어를 더 크게 측정한다.
Square-root mean squared error와 square-root relative squared error가 자주 쓰인다. (예측 값과 동일한 크기를 얻기 위해서, square와 root 상쇄되어 자연스러운 결과 얻음)

Evaluating the Accuracy of a Classifier or Predictor

a. Holdout Method

주어진 데이터를 랜덤하게 training set, test set으로 분리한다.
Random subsampling: holdout의 변형
- Holdout을 k번 반복한다.
- 정확도는 얻어진 k 개의 평균을 취한다.
데이터가 적다면 쓰기 어렵다. 데이터의 1/3이나 학습에 사용하지 못하기 때문이다.

b. Cross Validation

k-fold라고도 하며, k=10이 자주 쓰인다.
랜덤하게 데이터를 동일하게 k 개로 나눈다.(서로 교집합 없이)
i-th iteration에는 D_i를 테스트셋으로 하고 나머지는 트레이닝셋으로 한다.
- K=10이라면, 10%는 테스트셋, 90%는 트레이닝셋으로 사용하면서 10번을 각각 다른 테스트셋을 선정하여 반복하는 것이다.
Accuracy는 결국 k 개의 테스트 결과의 평균이 된다.
Holdout과 달리 모델을 만들 때 데이터를 더 많이 사용한다. 그렇기 때문에 더 적은 데이터에서 사용하기 좋다.

c. Leave-one-out

위의 cross-validation의 특별한 케이스로 데이터가 더 적을 때 용이하다.
k-folds를 하는데 k를 데이터의 수 즉, 튜플의 수를 사용한다.

d. Stratified cross-validation

Cross-validation의 특별한 케이스로 층이 있게 즉, 각 fold의 클래스 분포가 같아지도록 분배한다.
예를 들어, positive=70%, negative=30% 이면, 각 fold의 데이터들도 이 비율을 이루도록 분배한다.
데이터가 한 곳으로 몰리는 현상을 방지한다.

e. Bootstrap

작은 데이터셋(불충분한 트레이닝 샘플)인 경우 잘 작동한다.
전체 데이터셋에서 트레이닝 샘플을 골라낼 때, 한 번 골랐던 샘플도 다시 선택될 수 있도록 한다.
- .632 bootstrap: 가장 흔한 bootstrap 방법
  - 데이터셋이 d 개의 샘플로 이루어져있으면, d번 샘플되고 한 번 골라졌던 것도 다시 고를 수 있다.
  - 전체 데이터에서 마지막까지 뽑히지 않은 것은 테스트셋으로 분류한다.
  - 대략 전체 데이터의 63.2%가 트레이닝셋으로 분류되고 36.8%가 테스트셋으로 분류된다. (1- 1/d)^d는 약 e^-1 = 0.368 이기 때문
  - 샘플링하는 과정을 k번 반복하며 모델의 정확도는 i=1~k에 대하여
    acc(M) = 1/k * sum(0.632 * acc(M_i)_{test_set} + 0.368 * acc(M_i)_{train_set}))

Ensemble Methods

여러 모델들의 조합으로 정확도를 높이는 방식이다. k 개의 학습된 모델들을 결합해서 개선된 모델 M*을 만든다.

유명한 ensemble 기법으로는

Bagging: 분류기의 예측 평균
Boosting: 분류기의 가중 투표
Ensemble(좁은 의미): 다른 종류의 분류기 결합

등이 있다.

a. Bagging: Bootstrap Aggregation

여러 분류기의 예측값의 평균, 가장 많은 값을을 내는 것으로 의사들에게 진찰을 받는 상황을 생각해 볼 수 있다. 본인이 심각한 병에 걸렸다면 여러 명의를 찾아다며 진료를 받을텐데 여러 의사들이 입을 모아 이야기한 것을 믿지 않을텐가

결국 “의사들의 가장 많은 투표를 차지한 진단으로 결정한다”로 생각할 수 있다.

Bootstrap 방식으로 트레닝셋을 정한다.(D개의 튜플들 중 중복허용해서 d번 뽑는다)

Classification
그렇게 만들어진 트레이닝 셋마다 각각 분류모델을 만들고 각 분류기 M_i는 unkown 샘플 x에 대해서 class prediction을 한다.

Bagged classifier M*는 각 분류기의 결과값을 모아서 그 중 가장 많이 표를 받은 클래스를 리턴한다.

Prediction 주어진 테스트 튜플에 대한 각 예측값의 평균을 취하여 연속값 예측에 적용할 수 있다.

Accuracy 일반적으로 단일 분류기보다 더 좋을 때가 많다. Noise data에 대해 robust해서 나쁘지 않다. Prediction에 있어서 개선된 정확도를 보인다.

b. Boosting

여러 분류기마다 가중치를 매긴 결과이다. 앞선 의사의 예시를 여기서도 적용해보자. 명의도 명의대로 실력 차이가 있을 것이고 아무래도 더 명성이 높은 의사의 말을 신뢰할 것이다.

Boosting은 과거 진단 기록을 바탕으로 더 정확한 진단을 하는 의사에게 높은 가중치를 주어 진단을 결정하게 한다. 구현에 있어서는 실제로 높은 값을 주는 것은 아니고 틀린 분류를한 분류기에게 높은 가중치를 주는 식이다.

각 트레이닝 튜플에 가중치가 할당된다. 처음에는 가중치가 모두 같지만 이는 parameter이다. (학습하며 값이 변함)

k 개의 분류기가 반복적으로 학습한다. 분류기 M_i가 학습된 후, M_i+1을 학습시킬 때에는 이전 분류기에서 잘못 분류된 트레이닝 튜플에 더 큰 가중치를 부여함으로써 트레이닝 샘플로 뽑힐 가능성을 높여준다. 결국 가중치를 높여서 점점 여러 모델에 반영되게 한다.

최종 모델 M*은 각 분류기의 결과를 결합한 것이다.

새로운 데이터를 어떻게 분류하는가?

k 개의 분류기의 결과는 가중치(위에서 샘플에 사용된 가중치와 다름)이고 그 값이 가장 큰 값의 class label로 분류된다.