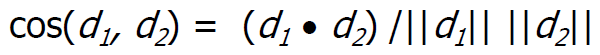[데이터 사이언스] Getting to know your data

in CS Review on DataScience


Chapter 2. Getting to know your data

  • Data Objects and Attribute Types
  • Basic Statistical Descriptions of Data
  • Data visualization
  • Measuring Data Similarity and Dissimilarity

Data Objects and Attribute Types

데이터가 어떻게 생겨먹었는지를 알아야 어떤 기법을 적용할 지 판단하기 쉽다!!

Types of Datasets.

Data는 application에 따라서 매우 다양하게 생겼다.

  • Record(Real-world entity에 대응)
    • Attribute 값들로 이루어져 있는 row
    • Relational records / Data matrix
      • Text documents: term-frequency vector
    • Transaction data
  • Graph and network
    • Node는 real-world entity, edge는 relationship
    • Social or information networks(유저가 node, 친구관계가 edge)
    • World Wide Web(웹페이지가 node, 하이퍼링크가 edge)
    • Molecular Structures(분자가 node, 분자 간의 관계가 edge)
  • Ordered(순서가 중요!!)
    • Video data: sequence of images
    • Temporal data: time-series
    • Sequential data: transaction sequences
    • Genetic sequence data
  • Spatial, Image and Multimedia
    • Spatial data: maps
    • Image data
    • Video data

위와 같이 실제로 data의 생김새와 특성은 매우 다양하며 그에 걸맞는 알고리즘들이 필요하다.

Important Characteristics of Data

  • Dimensionality
    • Curse of dimensionality(차원의 저주): dimension이 너무 커지면 발생하는 문제로, 차원이 작을 때는 잘 작동하다가 차원이 커지면 잘 작동하지 않는다. 예시로, 1차원 상에서는 거리 차이가 제일 작은 쌍과 큰 쌍이 있다고 하자. 이 때의 거리 차이는 크겠지만 고차원에서는 그 두 쌍의 차이가 별로 나지 않는 상황을 생각해 볼 수 있다.
  • Sparsity
    • 데이터가 많이 비어있는 상태(희소 행렬)
    • density가 낮으면(sparse하면) 데이터를 분석하기 어렵다.
  • Resolution
    • Resolution에 따라 pattern이 상이한 상황
  • Distribution
    • Centrality(중심성), Dispersion(중심으로부터 얼마나 퍼져있는가)

Data Objects

  • 데이터셋들은 여러 데이터 오브젝트(실세계 객체)들로 이루어져 있다.
    • Sales database: 고객, 아이템, 판매
    • Medical database: 환자, 처방현황
    • University database: 학생, 교수, 강의
  • Tuples, samples, examples, instances, data points, objects라고도 한다.
  • Data objects들은 Attribute들로 이루어져있다.
  • DB에서의 rows -> data objects
  • DB에서의 Columns -> attributes

Attributes & Attribute Types

특정 데이터 오브젝트의 특징을 설명하는 특성으로 dimensions, features, variables라고도 한다.

데이터 객체의 특성 또는 특징을 나타내는 data field이다.
ex) customer _ID, name, address

  • Attribute Types
    • Nominal: 카테고리, 상태, 어떤 것의 이름 등
      • 값의 수, 가짓수가 유한하다.
        • ex) Hair_color={black, blond, brown, grey, red, white}와 같이 유한한 상태로 제한된 attribute
      • 결혼 여부, 직업, 신분증 번호, 우편 번호 등이 nominal에 해당한다.
      • Attribute간의 우열을 가릴 수 없다.
    • Binary: 2 가지 상태(0 또는 1)만 가지는 nominal attribute의 특별한 케이스
      • Symmetric binary: 두 가지 값이 중요도가 같고 대등한 경우 ex) gender
      • Asymmetric binary: 중요도가 동등하지 않은 경우 ex) medical test(양성 vs. 음성)
        • 중요한 결과에 1을 할당(HIV 양성이면 1, 음성이면 0)
    • Ordinal
      • 값들이 중요한 순서를 갖고 있다. (Ranking)
      • 값을 구분할 수는 있지만(우열이 존재) 연속된 값들이 얼마나 차이가 있는 지 그 Magnitude는 정의되어 있지 않다.
      • Size={small, medium, large}, Grades={A0, A+, B0, B+…}, Army rankings
      • 학점의 경우 그 숫자 자체에서의 Magnitude가 아니라 예를 들어, A+맞은 학생이 B+맞은 학생보다 얼마나 잘하는 지를 모른 다는 것이다. 4.5만점 기준으로 1.0만큼 잘하는 게 아니지 않은가!!
    • Numeric
      • Quantity
        • 양이 있는 attribute(Integer or real-valued)
      • Interval-scaled
        • 값들에 순서가 있다.
        • 앞선 ordinal attribute와 달리 equal-sized units(magnitude가 일정하다), 값들의 차이를 알 수 있음 ex) 섭씨, 화씨 온도, 달력 날짜
        • 진정한 의미의 zero-point가 존재하지 않는다. 0도는 온도가 없는 것이 아님을 예로 들 수 있다.
        • 결과적으로, ratio-scaled는 아니다. “10 ℃가 20 ℃보다 10 ℃ 더 높다”라고 말할 수는 있지만 절대 영점이 없으므로 “10 ℃가 20 ℃보다 2배 더 높다”라고는 말하지 못한다
      • Ratio-scaled
        • 진정한 zero-point가 존재한다.(없음을 의미하는 zero가 정의되어 있음)
        • 임의의 값 사이에 규모가 얼마나 차이나는지 알 수 있다. 즉 배수가 의미있다. ex) 6kg은 3kg의 2배
        • ex) 켈빈온도, 길이, 개수, 돈

    • Discrete vs Continuous Attributes

      • Discrete Attribute
        • 유한하고 셀 수 있는 값들, 가끔 정수 변수로 표현
          • 우편번호, 단어 수 등
        • Binary attribute는 discrete attributes의 특별한 케이스
      • Continuous Attribute
        • Attribute 값으로 실수값을 가진다. 즉, 무한하다 ex) 온도, 높이, 무게
        • 실제로, 실제 값은 한정된 자릿수를 사용해서만 측정되고 표현될 수 있다.
        • 연속형 속성은 일반적으로 부동 소수점 변수로 표현된다.

Basic Statistical Descriptions of Data

데이터의 기본적인 통계에 대해 왜 알아야할까?

데이터를 보다 잘 이해하기 위해서이다. 예로, 중심적인 경향과 그 중심으로부터 데이터가 얼마나 퍼져있는 지 등을 알 수 있기 때문이다. 이를 대략 알고 있다면 알고리즘을 올바르게 적용할 수 있다.

데이터 분산의 특성으로는 median, max, min, quartiles(4분위수), outliers, variance 등이 있다.

Measuring the Central tendency

데이터의 중심적인 경향을 나타내는 것으로 mean, median, mode가 있다.

  • Mean(Algebraic measure)
    • Sample의 mean: (샘플인 x의 합) / (x의 개수)
    • Population(전체)의 mean: (전체 x의 합)/(전체 x의 개수)
    • 전체 크기인 경우는 N, 샘플의 크기인 경우는 n으로 표기한다.
      • Weighted arithmetic mean: 샘플마다 중요도를 반영한다. 예시로, 국영수를 치뤘을 때 수학에 더 비중이 있다면 weight을 다르게 처리해주는 것이 있다.
      • Trimmed mean: 너무 극단적인 값이 있다면 평균의 의미를 저해하므로 제외하고 계산한다. 적절한 기준을 설정하기 어려우므로 잘 사용하지 않는다.

Mean은 Outlier에 영향을 많이 받는다는 단점이 있어 Median이라는 척도가 생겼다.

  • Median
    • 정렬이 되어 있다는 전제하에, 홀수개의 데이터인 경우 가장 가운데 위치한 값, 짝수개의 데이터인 경우 가운데 위치한 두 값의 평균을 말한다.
    • Outlier에 robust하다는 장점이 있다.
    • 새로운 값이 들어온다면, 매번 들어올 때마다 정렬 후 구할 수 있기 때문에 overhead가 있다. 때문에, 이를 동적으로 처리해야하는데 그 방법으로 data를 그룹화(histogram)해서 interpolation으로 추정하는 방법(구간 안에서 uniform하게 분포한다고 가정)을 사용한다.
    • 처음에 구간을 나누고 도중에 새로운 데이터가 들어오면 그 데이터가 해당하는 구간의 frequency를 올려준다.
    • Median = L1(구간의 시작지점) + ((n/2-sum(이전 freq))/(median frequency)) x width

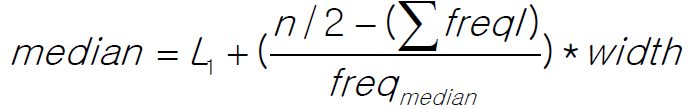
Median

위 식을 예로 적용해보자. 우선, 아래와 같이 데이터를 그룹화한다.

agefrequency
1-5200
6-15450
16-20300
21-501500
51-80700
81-11044

L1 = 21, n = 3194, Median = 21 + ((1597-(200+450+300))/(1500))x(50-21)

  • Mode
    • 가장 데이터에서 많이 등장하는 값(최빈값)
    • 가장 빈도 높은 것 1(Unimodal), 2(Bimodal), 3(Trimodal)개 선택
    • Empirical formula
      • 일반적인 특성으로 아래 식을 따르는 경향이 있다. 항상 만족하지는 않는다.

        mean-mode = 3 * (mean-median)
        평균에서 최빈값 뺀 것은 평균에서 중앙값 뺀 것의 3배이다.

  • Symmetric vs. Skewed data
    위의 식에서 2개를 알고 있으면 나머지 하나를 예측할 수 있다.

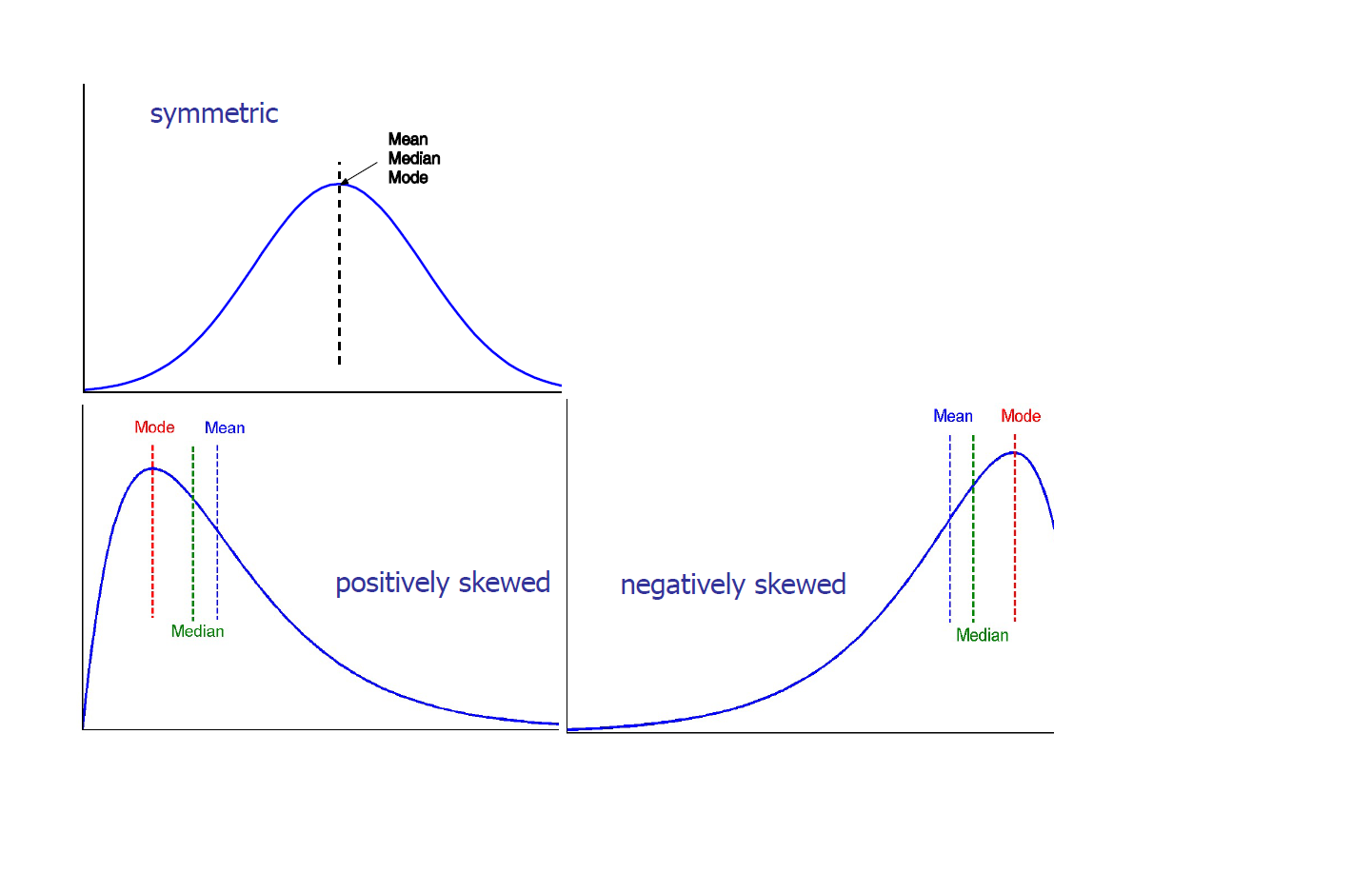
Symmetric vs. Skewed Data

  • Symmetric인 경우는 mean, median, mode 모두 같은 경우이다.
  • Skewed인데 mean > median > mode인 경우, positively skewed이고 반대로 mode > median > mean인 경우, negatively skewed이다.

Measuring the Dispersion of Data

  • Measurement
    • Quartiles: Q1(25th percentile) / Q3(75th percentile) / Q2(50th percentile = median) / Q4(100th percentile = max)
    • Inter-quartile range(IQR): IQR = Q3-Q1, 이 차이가 작으면 데이터가 조밀하게 분포한 것이고 크다면 넓게 분포한 것을 뜻한다. 해당 구간에 전체 데이터의 50%가 속한 것이기 때문이다.
    • Five number summary: min, Q1, median, Q3, max
    • Boxplot: Five number summary를 시각화 한 것이다.

    • Outlier: 주로 값이 1.5 x IQR보다 같거나 큰 값

    • Variance and standard deviation
      • Variance: 평균에서 각각의 값이 얼마나 떨어져 있는가를 제곱으로 나타낸 것을 말한다.
      • Sample: s, Population: sigma
      • Sample(s)의 Variance(Algebraic, scalable computation): 편차 제곱의 평균인데 통계적으론 n이 아닌 n-1로 나눈다. 자세한 내용은 여기서!!!
      • 전체 데이터(N)의 variance
      • Standard deviation: 평균에서 각각의 값이 얼마나 떨어져 있는가를 나타내는 값으로, 값이 작다면 매우 촘촘한 것이고 크다면 널리 떨어져 있는 것을 뜻한다. s 또는 시그마(variance의 루트)로 표현
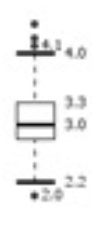
  • Boxplot Analysis
    • Five-number summary(minimum, Q1, median, Q3, Maximum)
    • Boxplot
      • 데이터를 box로 표현한다.
      • Box의 왼쪽 끝은 Q1, 오른쪽 끝은 Q3로, 박스의 길이가 결국 IQR이 된다.
      • Median은 box안에 선으로 표기한다.
      • Minimum, maximum은 박스 바깥 선으로 연결하여 표시한다.
      • Outliers: outlier threshold를 넘어간 곳에 점으로 표기한다.

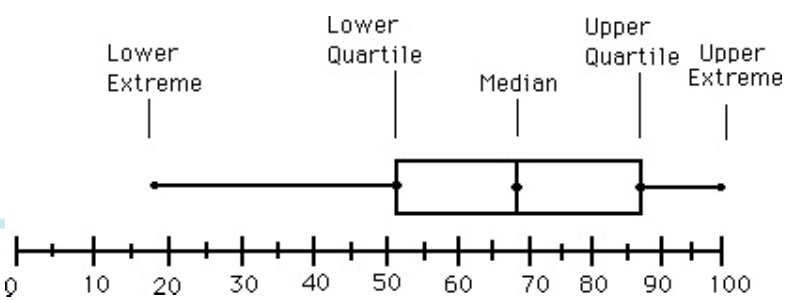
    Boxplot Analysis

위의 그림 예시에서는 outlier(IQR의 1.5배)가 길이를 초과하므로 없다. Outlier가 있는 예시는 아래와 같은 그림이 있다.
Boxplot Outlier

Properties of Normal Distribution Curve

  • The normal (distribution) curve
    • 뮤: mean, 시그마: 표준편차
    • 뮤-시그마 to 뮤+시그마: 전체 데이터의 68%를 포함한다.
    • 뮤-2시그마 to 뮤+2시그마: 전체 데이터의 95%를 포함한다.
    • 뮤-3시그마 to 뮤+3시그마: 전체 데이터의 99.7%를 포함한다.

Data Visualization

Graphic Displays of Basic Statistical Descriptions

1. Boxplot
Five number summary인 5개의 숫자(min, Q1, median, Q3, max)를 시각적으로 보여준다.

2. Histogram
x축은 값, y축은 빈도를 나타내는 막대 형태의 그래프로 data distribution을 한눈에 파악할 수 있다.

  • 히스토그램에서의 막대는 서로 인접해있고 겹치지 않는다.
  • 각 category(구간)에 속하는 case들의 비율(얼마나 많은가)을 보여준다.
  • Bar chart와의 차이
    • Bar chart는 높이(y값)가 그 값을 나타낸다. 즉, 가로를 신경쓸 필요가 없다.
    • 히스토그램은 넓이가 그 값을 나타낸다. 즉, 가로를 신경써야 한다.
    • Bar chart는 histogram의 special case이다.

3. Quantile plot
기본적으로, 하나의 attribute에 대해 모든 데이터를 표시한다. User로 하여금 전체적인 경향이나 경향에 어긋나는 케이스들을 확인하기 쉽게 한다.

f-value를 0, 0.25, 0.5, 0.75, 1.00에 눈금을 만들어서 quantile 정보를 알게한다. 이 때, 데이터 Xi는 오름차순으로 정렬하고 그에 따른 f는 0~1의 값으로 100%에 곱해서 값의 위치를 구할 수 있다.

4. Quantile-quantile(q-q) plot
다른 두 데이터 셋을 같은 attribute에 대해 비교할 때 사용한다. 한 분포의 quantiles와 이에 대응하는 다른 분포의 quantiles를 표기한다.

예를 들어, branch1, branch2(각각 다른 분포의 attribute)가 있으면 branch1 축의 40~120 값의 분포에 대해 branch2는 어떻게 분포하는지 점으로 표기한다. 아래의 그림을 보면 이해하기 쉽다. 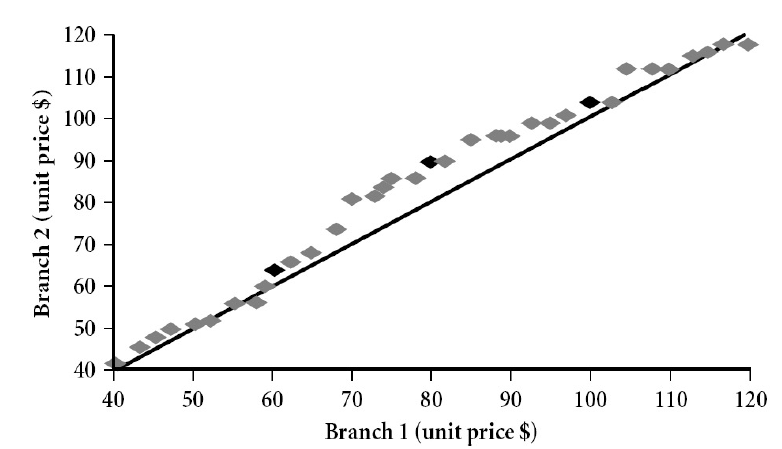QQ Plot

5. Scatter plot
하나의 데이터셋에서 서로 다른 2 개의 attribute에 대해 관계를 알고 싶을 때 사용한다. 각 값 쌍은 한 쌍의 좌표이며 평면에 점으로 표현된다. 점, 특이치 등의 군집을 확인할 수 있는 이변량 데이터를 한눈에 보여준다. 또 이를 바탕으로, positively & negatively correlated data인지를 확인할 수 있다. 당연히 아무런 correlation이 없는 경우도 있다.

Measuring Data Similarity and Dissimilarity

Similarity and Dissimilarity

  • Similarity
    • 두 data objects가 얼마나 비슷한지 수치로 나타내는 것
    • 두 objects가 비슷할수록 더 값이 크다.
    • 주로 0~1 사이의 값을 갖게끔 한다.
  • Dissimilarity
    • 두 data objects가 얼마나 다른지 수치로 나타내는 것
    • 두 objects가 비슷할수록 더 값이 작다.
    • 같은 object인 경우 0값을 갖는다. 즉, minimum dissimilarity는 주로 0이다.
    • 예로, 거리를 들 수 있다.
    • 상황에 따라 upper limit이 다르게 설정된다.
  • Proximity
    • similarity나 dissimilarity를 둘 다 나타낸다.

Data matrix and Dissimilarity matrix

  • Data matrix
    • n개의 데이터마다 가지는 p개의 attribute들을 나타낸다.
    • 한 row가 하나의 데이터를 나타내며 전체 row는 전체 데이터 샘플을 나타낸다.
    • column별로 애트리뷰트의 값이 저장되어있는 행렬이다.
    • Two modes: 한 차원은 sample, 다른 한 차원은 attribute를 나타낸다.
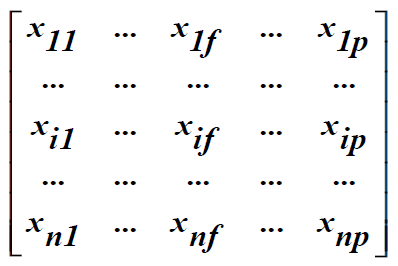
      Data matrix
  • Dissimilarity matrix
    • n개의 데이터가 있으나 pair마다 distance만을 저장한다.
    • Symmetric하기 때문에 triangular matrix이다.
    • Asymmetric할 때에는 사용하지 않는다.(순서가 바뀌어도 거리가 일정해야 함)
    • Single mode: 두 차원 모두 object를 나타낸다.
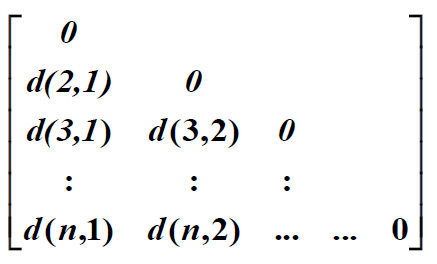
      Dissimilarity matrix

Proximity Measure

1. For Nominal Attributes
Binary attribute의 일반화로 2 개 이상의 상태를 갖는 attribute에 대해선 2 가지 방법이 있다.

  • Method 1: Simple matching
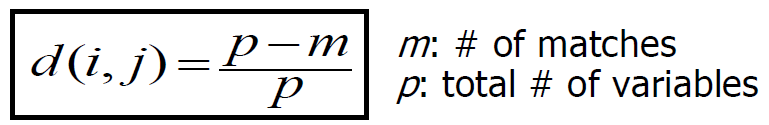
    Simple matching
  • Method 2: 여러 개의 Binary attribute들을 사용
    • 각 M개의 nominal state에 대해서 binary attribute를 생성한다.
    • 예를 들어, yellow이면 1이고 나머지 red, blue, green은 0으로 나타낸다.

2. For Binary Attributes
Binary attribute를 위해서 contingency table을 만든다.
Contingency table
Object i와 j에 대한 표이다. Binary attribute일 때, 둘 다 1인 data가 q개이고 나머지도 그런 식으로 해석하면 된다.

  • Symmetric binary variables를 위한 distance measure
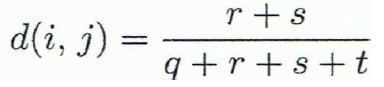
    Symmetric binary
  • Asymmetric binary variables를 위한 distance measure
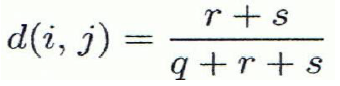
    Asymmetric binary
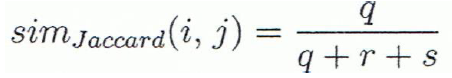
  • Asymmetric binary variables의 similarity를 측정하는 도구로 Jaccard coefficient가 있다. 그냥 1 - d(i,j)를 하면 된다. Jaccard coefficient

요약하자면, 대칭인 것은 다 더해서 값이 서로 다른 것의 비율을 구하고 비대칭인 것은 둘 다 0인 것을 제외하고 서로 다른 것의 비율을 구하는 것이다.

Standardizing Numeric Data

  • Z-score
    • z = (X-뮤)/std
    • X: Standardized할 raw score
    • 뮤: 전체 데이터의 평균
    • std: 표준편차
    • raw score와 평균의 거리를 표준편차의 단위로 측정한 것이다.
    • 음수이면 평균 아래이고, 양수이면 평균 위이다.
  • 다른 방법으로 mean absolute deviation을 계산하는 방법이 있다.
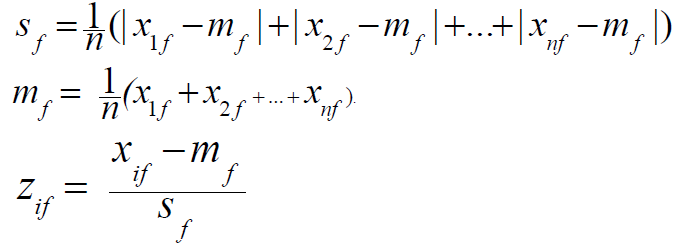
    Mean absolute deviation
    • Outlier가 존재할 때, Mean absolute deviation을 사용하면 standard deviation을 사용할 때보다 더 robust하다.

Distance on Numeric Data: Minkowski Distance

  • Minkowski distance(L-h norm)
    • Distance를 구하는 방식으로, 다음 식을 따른다.
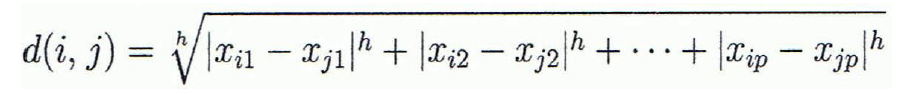
      Minkowski Distance
    • 다음 3 가지 Properties가 있다.
      • i와 j가 같지 않다면 항상 0보다 크다. (Positive definiteness)
      • i에서 j까지의 거리와 j에서 i까지의 거리가 같다. (Symmetry)
      • i에서 j까지의 거리는 i에서 k까지의 거리와 k에서 j까지의 거리보다 항상 작거나 같다. (Triangle Inequality)
      • 위 3 가지 properties를 만족하는 distance를 metric이라고 한다.
  • Special Cases of Minkowski Distance
    • h=1일 경우: Manhattan distance
    • h=2일 경우: Euclidean distance
    • h=max(무한대)일 경우: Supremum distance(벡터 안의 어느 성분끼리든 차이가 가장 큰 값)

Ordinal Variables

  • 순서가 중요한 attribute이다. ex) rank
  • Interval-scaled로 바꿔 생각한다.
    • xif를 rank로 값을 바꾼다.
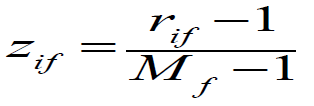
    • 값을 0~1사이의 범위로 매핑한다. Interval scaled
    • rif는 값의 rank이다.
    • Mf는 highest rank의 값이다.
    • 위 방식으로 dissimilarity를 계산한다

Attributes of Mixed Type

DB가 다양한 attribute type들을 가질 것이다. ex) Nominal, symmetric binary, asymmetric binary, numeric, ordinal …

이 때에는 weighted formula를 사용한다. 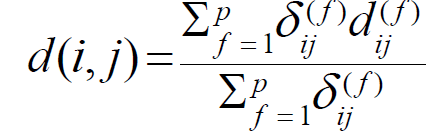Weighted formula

  • f가 binary, nominal인 경우: xif=xjf라면 dij(f)=0, 서로 다르면 1이다.
  • f가 numeric인 경우, normalized distance를 사용한다.
  • f가 ordinal인 경우, 위에서 처럼 rank를 게산하고 zif를 계산한다.

Cosine Similarity

Document마다 각 단어의 빈도수(term-frequency)를 기록한 행렬이 있다고 하자. 하나의 Document가 다른 document의 두 배라면 similarity는 비슷해야 하는데, Euclidean으로 계산하면 값이 너무 커지는데 이를 해결하기 위해 cosine similarity를 사용한다.

d1과 d2 2 개의 벡터(Term-frequency vectors)가 있다고 하자. 그럼, cosine similarity는 (d1과 d2의 내적)/||d1||x||d2||로 계산할 수 있다.

Weighted formula