[데이터 사이언스] Cluster Analysis

in CS Review on DataScience


Chapter 7. Cluster Analysis

  • What is Cluster Analysis?
  • Types of Data in Cluster Analysis
  • A categorization of Major Clustering
  • Partitioning Methods
  • Hierarchical Methods
  • Density-Based Methods
  • Outlier Analysis

What is Cluster Analysis?

Cluster Analysis는 무엇일까? 먼저 cluster가 뭔지 살펴보자. Cluster란 군집이라고도 하는데, 결국 data object들의 모임을 말한다. 같은 cluster 안에 있으면 서로 비슷한 것을 뜻하며 반대로 서로 다른 cluster라면 비슷하지 않은 것이다.

이러한 cluster를 분석한다는 것은 즉, 데이터의 특성을 바탕으로 데이터 간의 유사도를 구하는 것이다. 유사도를 구해서 비슷한 data object들끼리 묶어주기 위함이다.

Cluster analysis는 unsupervised learning의 한 종류로 학습 시 데이터에 정의된 클래스가 없다. 이는 데이터 분포에 대한 insight를 얻을 수 있는 stand-alone tool이며 주로 다른 알고리즘을 위한 전처리 과정에 해당된다.

사용 예시로는 Spatial Data analysis, Economic Science(like market research), WWW(Cluster documents, weblog data), Image processing & pattern recognition 등이 있다. 이외에도 marketing, land use, insurance, city-planning이 있다.

Quality and Requirements of Clustering

“Good” clustering method는 높은 quality의 cluster를 제공하는데, 서로 다른 클래스 간에 낮은 유사도(low inter-class similarity) 혹은 하나의 클래스 안에서 높은 유사도(high intra-class similarity)를 보이는 것을 말한다.

결국 clustering의 결과의 quality는 similarity measure와 method로 결정된다. Clustering method의 quality는 숨겨진 패턴을 발견하는 능력에 의해 결정된다.

Clustering의 quality를 측정하려면 similarity/dissimilarity metric을 알아야 한다. Similarity는 distance function으로 d(i,j)로 표현하곤 한다. 변수 타입(interval-scaled, boolean, categorical, ordinal ratio, vector variables)에 따라 다르고 “충분히 유사하다” 혹은 “충분히 좋다”를 정의하기란 매우 주관적이다. 가중치는 attribute마다 다른 가중치를 가질 수 있다.

Data mining에서 clustering의 Requirements는 아래와 같은 것들이 있다.

  • 서로 다른 타입의 attribute들을 처리할 수 있어야 한다.
  • 새로운 데이터가 추가되거나 기존의 데이터가 지워지더라도 잘 동작할 수 있어야 한다. (= Dynamic)
  • 임의의 모양의 cluster를 발견할 수 있어야 한다.
  • 파라미터를 정하는 데에 domain knowledge가 많이 필요해서는 안된다.
  • Noise와 outlier를 처리할 수 있어야 한다.
  • 입력 순서와 상관없이 동일한 결과를 출력해야 한다.
  • 높은 차원을 갖는(많은 attribute를 갖는) 데이터들도 처리할 수 있어야 한다.
  • Scalability
  • Incorporation of user-specified constraints

A Categorization of Major Clustering Methods

1. Major Clustering Approaches

  • Paritioning approach
    • 다양한 파티션을 구성하고 몇 가지 기준에 따라 평가한다.
    • Typical methods: k-means, k-medoids(PAM, CLARA)
  • Hierarchical approach
    • 어떤 기준으로 계층적으로 데이터를 분리한다.
    • Typical methods: DIANA, AGNES, BIRCH, ROCK, CHAMELEON
  • Density-based approach
    • 밀도함수를 기반으로 클러스터를 형성한다.
    • Typical methods: DBSCAN, OPTICS

2. Centroid, Radius, and Diameter of a cluster (For numerical data)

클러스터 내에서 centroid, radius, diameter의 정의!!

  • Centroid: 클러스터의 중간 지점
    • 각 애트리뷰트 값 끼리 더해서 평균을 구한다.
    • i: i th object, p: p th attribute라면, 아래와 같다.
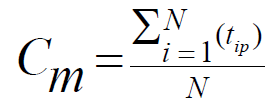
      Centroid

  • Radius: cluster의 모든 object에서 centroid까지 거리 제곱의 평균의 루트값
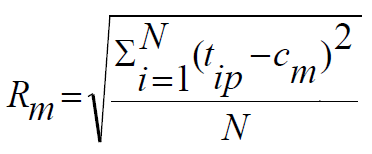
    Radius

  • Diameter: 모든 오브젝트 쌍들의 거리 제곱의 평균의 루트값
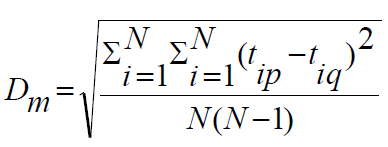
    Diameter

클러스터 간의 거리를 계산하는 일반적인 대안으로 여러 가지 방식이 있다.

  1. Single link: 모든 가능한 쌍에 대해, 한 클러스터의 원소와 다른 클러스터의 원소 사이의 최소 거리
    • dis(Ki, Kj) = min(tip, tjq)
  2. Complete link: 모든 가능한 쌍에 대해, 한 클러스터의 원소와 다른 클러스터의 원소 사이의 최대 거리
    • dis(Ki, Kj) = max(tip, tjq)
  3. Average: 한 클러스터와 다른 클러스터 각각에서 원소를 하나씩 뽑은 모든 쌍에 대해서 거리를 구한 후 평균을 구한 것
    • dis(Ki, Kj) = avg(tip, tjq)
  4. Centroid: 두 클러스터의 centroid 사이의 거리!
    • centroid는 실제 object가 아니라 위치를 나타낸다.
    • dis(Ki, Kj) = dis(Ci, Cj)
  5. Medoid: 두 클러스터의 medoid 사이의 거리!
    • dis(Ki, Kj)=dis(Mi, Mj)
    • Medoid: 클러스터에서 가장 가운데에 위치한 실제 object

Partitioning Methods

1. Basic Concept

  • Database D에서 n개의 objects를 k개의 클러스터로 나누는 것으로, 클러스터를 대표하는 값과 그 클러스터의 모든 objects 까지 거리의 제곱의 합이 최소가 되도록 한다. 아래의 함수가 goodness function으로 이 값이 최소가 될수록 좋다고 할 수 있다.
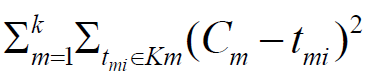
    Partitioning method
  • 모든 파티션을 다 살펴보면 global optimal을 찾을 수 있겠지만 heuristic methods를 사용한다.
    • K-means: 각 cluster는 cluster의 centroid로 표현된다.
    • K-medoids or PAM(Partition around medoids): 각 cluster는 cluster의 object 중 하나로 표현된다.

2. The K-Means Clustering Method

K값이 주어졌을 때 다음과 같이 진행된다.

  • objects를 임의로 k 부분으로 나눈다. 임의의 k 점을 initial cluster center로 하여 다른 모든 점들을 할당하여 cluster를 만드는 것이다.
  • k 부분으로 나눠진 각 클러스터에 대해서 centroid(center로 cluster의 mean point) 값을 계산한다.
  • 각 objects를 가장 가까운 seed point(centroid)의 클러스터로 다시 포함시킨다.
  • 다시 centroid값을 계산으로 돌아가는 과정을 반복하여 클러스터가 바뀌지 않을 때까지 진행한다.

K-means는 상대적으로 효율적이다. 시간복잡도가 O(n * k * t)이다. n은 object의 수이며 k는 cluster의 수이고 t는 반복 횟수이다. 일반적으로 n이 다른 두 수보다 매우 크다. 그렇기에 K-means는 거의 linear하다고 볼 수 있다. PAM(=O(ik(n-k)2)), CLARA(=O(ks2+k(n-k)))와 비교해보면 상대적으로 효율적임을 알 수 있다.

하지만 종종 local optimum으로 빠진다는 문제가 있다(모든 object 기준에서 계산하는게 아닌 초기에 정한 seed로부터 계산되기 때문). 또한 categorical data인 경우는 적용할 수 없다. Mean을 정의할 수 있어야 하기 때문이다. 결과적으로 numerical attribute와 같은 타입에 적용 가능하다. 또한 사전에 k 값을 정해주어야 하는데 까다로울 수 있으며 noise와 outlier를 잘 처리하지 못한다는 단점이 있다. Non-convex shape인 cluster를 발견하기에 적절하지 않다. Centroid를 중심으로 cluster를 만들어나가기 때문이다.

이러한 K-Means method의 변형으로 2 가지가 있다. 앞서 categorical data를 처리하지 못하니까 이를 해결하고자 k-modes가 나왔다. Centroid 대신에 modes(최빈값)을 사용한다.

  • X, Y: m 개의 categorical attribute를 갖는 object들
  • Dissimilarity d(X, Y): # of total mismatches
  • Mode는 해당 object와의 mismatch 수의 합이 가장 작은 object(벡터)이다.
  • X라는 cluster를 구한다면, Attribute마다 가장 자주 발생하는 값을 가져온다.
  • frequency-based method을 사용하여 cluster의 mode를 갱신한다.

일반적으로 데이터는 categorical과 numerical data가 섞여있으므로 k-prototype method를 사용한다.

K-Means method의 문제점으로 outlier에 너무 민감한 점을 꼽을 수 있다. Outlier 때문에 클러스터가 잘못 분리하여 왜곡할 수 있다.

이 때문에 K-Medoids라는 방식이 나왔는데, cluster 내 object의 평균값(centroid)을 기준점으로 삼는 대신에 cluster 내 가장 중앙에 위치한 object(medoid)를 사용할 수 있다.

3. The K-Medoids Clustering Method

K-Medoids clustering method로는 다음 2 가지 방식이 있다.

  1. PAM(Partitioning Around Medoids)
  2. CLARA(Clustering Large Applications)

PAM(Partitioning Around Medoids)

1) 실제 object를 cluster의 대표값으로 선정하는데, k 개의 object를 임의로 선택한다.
2) 선택된 object(seed)를 i, 선택되지 않은 object들을 h(새 seed의 후보)라고 할 때, swapping cost TCih을 각 pair i,h에 대해 계산한다.
3) 만약 TCih이 음수라면 i는 h로 바뀌고 선택되지 않은 object들은 가장 가까운 object로 할당된다.
4) 위 과정을 변화가 없을 때까지 반복하는 것이 알고리즘이다.

선택되지 않은 각각의 object j마다 i 대신 h를 medoid로 했을 때 j가 속하는 medoid까지와의 거리 d(j,h)와 기존에 할당되어있던 j의 medoid까지의 거리 d(j,i)의 차를 구하고 이들의 합이 total swapping cost이다. 아래 그림은 i가 original seed이고, h는 새로운 seed, t는 다른 seed, j는 seed가 아닌 점이다.
PAM 1

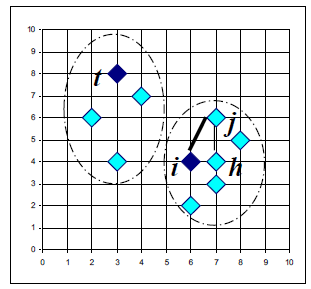
만약 object j의 medoid가 i가 h로 바뀌는 것에 상관없이 동일하다면 해당 cost는 0이 된다.
PAM 2

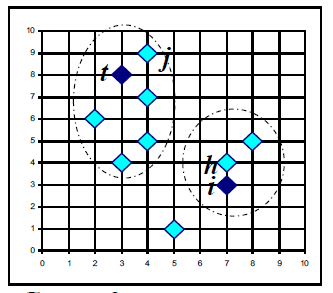
이러한 PAM은 k-means보다 noise나 outlier에 robust하다는 장점(medoid는 mean이 아닌 median과 닮아서)이 있지만 크기가 큰 데이터셋에는 잘 작동하지 않는다. n은 data의 수, k는 cluster의 수, i는 iteration의 수라고 할 때 시간 복잡도는 O(i * k * (n-k)2)라고 표현할 수 있다.

이로 인해 CLARA라는 sampling based method를 사용하게 되었다.

CLARA(Clustering Large Applications)

데이터셋에서 여러 샘플들을 뽑아내고 각 샘플마다 PAM을 적용하여 클러스터 결과를 가져오는 방식으로 샘플링 덕분에 더 큰 데이터셋을 처리할 수 있게 되었다.

그러나 샘플 크기에 따라 효율성이 달라지며(샘플 크기가 너무 작으면 성능이 좋지 않다), 샘플이 편향되어 있다면 그 결과를 잘 뽑아도 전체 데이터셋 기준으로 보면 “good” clustering이라고 볼 수 없다. 결국, 샘플을 잘 뽑지 않으면 좋은 클러스터링을 할 수 없게 되는 것이다.

Hierarchical Methods

Clustering을 하는 기준으로 distance matrix를 사용한다. 앞선 k 어쩌구들처럼 k값을 정해줄 필요는 없지만, 종료 조건이 필요하다. 크게 두 가지 방식이 있다. Bottom-up과 Top-down 방식인데, 각각 agglomerative(AGNES), divisive(DIANA)라고 한다.

1. AGNES(Agglomerative Nesting)

Single-link method와 dissimilarity matrix를 사용한다. Single link method는 앞서 배웠듯, 모든 가능한 쌍에 대한 minimum distance 즉, 가장 유사도가 높은 클러스터끼리 혹은 가장 dissimilarity가 낮은 노드끼리 merge하는 방식이다.

계속 merge해나가므로 총 거리 cost는 non-descending하다. 결국엔 모든 노드가 같은 cluster에 속하게 된다.

처음 묶을 때 가능한 가짓수를 파악해야 하는데, n(n-1)/2가지의 조합을 살펴봐야 한다.

어떻게 cluster가 merge되는지 한눈에 쉽게 보기 위해 만든 것이 dendrogram이다. 클러스터가 merge되는 순서를 보여주며 특정 레벨에서 자르면 연결된 각 구성요소가 클러스터가 된다.

2. DIANA(Divisive Analysis)

앞서 소개한 AGENS과 반대 방향으로, 결국 각 노드가 하나의 cluster가 되는 꼴이다. 초기엔 주어진 모든 n 개의 object들로 이루어진 cluster가 있다. 각 step마다 제일 큰 cluster가 두 개로 나눠진다. 즉, n 개의 object라면 n-1 개의 step이 필요한 것이다.

처음 나눌 때 2n-1-1가지의 조합을 살펴보아야 한다. 앞서 배운 AGNES보다 상당히 큰 수이다. 결국, 모든 가짓수를 살펴보는 것은 너무 많으므로 이를 최대한 줄여야 하는데 다음과 같은 방법을 사용한다.

  1. 다른 모든 object와 average dissimilarity가 가장 큰 object를 찾고 이를 통해 새로운 cluster를 만드는데, 이를 splinter group이라고 하자.
  2. splinter group 바깥의 각 object i마다, Di를 계산한다.
    Di = [average d(i,j) which j not in splinter group] - [average d(i,j), which j in splinter group]
  3. Di가 가장 큰 object h를 찾고, 만약 Dh가 양수라면 h는 splinter group에 가까운 것이므로 splinter group에 포함시킨다.
  4. 2번과 3번을 Dh가 음수가 나올때까지 반복하고 음수가 나오면 그 전까지 분리된 그룹을 바탕으로 두 개의 클러스터로 나눈다.
  5. 가장 큰 diameter를 갖는 cluster를 선택(diameter가 가장 크다는 것은 그 클러스터 안의 임의의 두 개는 가장 큰 dissimilarity를 갖는다는 것이다)하고 1번부터 다시 시작한다.
  6. 모든 클러스터가 하나의 object만을 갖을 때까지 1~5번을 반복한다.

Advanced Hierarchical Clustering Methods

Agglomerative clustering method의 주요 문제점으로 많은 object들을 다루기 어렵다는 점이 있다. 시간 복잡도가 O(n2)으로 매우 높기 때문이다.

Distance-based clustering으로 이를 개선한 방식들이 있는데 다음 3 가지가 있다.

  1. BIRCH
  2. ROCK
  3. CHAMELEON

1. BIRCH

CF(Clustering Feature) 트리를 점진적으로 구성한다. 다단계 clustering을 위한 계층적 데이터 구조이다.
Phase 1: DB를 스캔하고 in-memory CF tree를 구성한다.
Phase 2: 임의의 clustering algorithm으로 CF tree의 leaf node들을 구성한다.

한 번의 스캔으로 양호한 clustering을 찾고(scales linearly), 몇 번의 추가 스캔으로 품질을 향상 시킬 수 있지만, numeric data만을 처리할 수 있으며 data record 순서에 민감하다.

Clustering Feature는 (N, LS, SS)로 이루어져있는데, N은 data point의 개수이고, LS는 dataset의 (각 좌표계끼리) 모든 합이고, SS는 dataset의 제곱의 합이다. 마찬가지로 각 좌표계끼리의 제곱이다.

LS를 N으로 나눈다면 centroid를 구할 수 있고, SS를 N(N-1)로 나누고 제곱근을 취하면 diameter를 구할 수 있다. 결국 clustering feature는 cluster에 대한 통계적 요약이며 cluster에 대한 중요한 측정값들을 기록하고 storage를 효율적으로 활용할 수 있게 한다.

CF tree는 hierarchical clustering을 위한 clustering feature를 저장하는 height-balanced tree이다. Leaf node가 아닌 노드는 자식이 있으며 자식들의 총 CF를 저장한다. 이러한 CF 트리에는 두 개의 파라미터가 있는데, branching factor와 threshold이다. Branching factor는 최대 자식 수를 명시하며, threshold는 leaf node에 저장되는 최대 diameter를 말한다.

1) DB를 scan하여 CF tree를 구성한다.
2) 초기에 첫번째 object를 추가하면 1개의 cf가 생긴다. (이때 n=1, linear=값 자신, square=자신의 제곱)
3) 여기서 하나 더 추가하면 n=2가 된다. 계속 반복하여 diameter가 threshold를 넘으면 split하여 또 다른 cf를 만든다.
4) cf를 계속 만들어가다가 branching factor를 넘으면 2개의 leaf node로 균형을 유지하며 분리한다.
5) 리프노드 만들고 또 넘치면 나누는 식으로 반복한다.

이 때, 임의의 클러스터링 알고리즘을 사용하여 리프노드를 clustering한다.

결과적으로, 시간 복잡도는 O(n)으로 많이 줄였다. 그러나 데이터 삽입 순서에 민감하고 leaf node의 크기를 고정하기 때문에 cluster가 자연스럽지 않을 수 있으며 cluster가 둥근 형태로 제한될 수 있다.

2. ROCK: RObust Clustering using linKs(clustering categorical data)

거리 기반이 아닌, link라는 개념을 사용하여 similarity와 proximity를 측정한다. Jaccard coefficient와 같은 categorical data에 대한 고전적인 measure는 잘 작동하지 않을 수 있다.

먼저, Jaccard coefficient를 기반으로 한 similarity function으론 아래와 같은 공식이 있다.
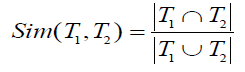
JC based similarity

예시로, T1={a,b,c}이고 T2={c,d,e}라면 similarity는 0.2이다.

이러한 jaccard coefficient의 문제점으로 intra class간의 similarity가 inter class간의 similarity보다 높은 경우가 발생할 수 있다.

Link란 common neighbor들의 수이다. 두 페어의 Jaccard coefficient가 0.5를 넘으면 common neighbor로 본다.

예로, T1={a,b,c}, T2={c,d,e}, T3={a,b,f}라고 하자. link(T1, T2)=4이다. 왜냐하면 이 둘은 {a,c,d}, {a,c,e}, {b,c,d}, {b,c,e} 4개의 공통된 neighbor가 있기 때문이다.

결과적으로, Jaccard coefficient보다 link를 통한 측정이 더 낫다고 볼 수 있다.

3. CHAMELEON: Hierarchical Clustering Using Dynamic Modeling

Dynamic model에 기반해서 similarity를 측정한다. Bottom-up 방식으로 두 클러스터는 interconnectivity와 closeness(proximity)가 충분히 높은 경우에만 병합된다.

충분히 높은 경우란 언제를 말하는 걸까? 바로 두 클러스터를 다시 각각 두 조각으로 쪼개서 interconnectivity와 closeness를 구하고 그것들보다 상대적으로 큰 경우를 말하는 것이다.

내부의 interconnectivity와 closeness보다 interconnectivity, closeness가 큰 클러스터끼리 합치는 것이다.

우선, 전체 데이터에 대해 k-nearest neighbor 그래프를 먼저 만든다. 이 때, 노드는 각각의 object를 의미하고, 간선은 k-nearest neighbor의 link(가장 가까운 k개의 object들을 잇는다)를 뜻하며, weight은 similarity가 된다.

2-phase 알고리즘으로 graph partitioning algorithm(작은 클러스터들을 생성)과 agglomerative hierarchical clustering algorithm(하위 클러스터를 반복적으로 결합하여 실제 클러스터를 찾음)을 사용한다.

  • Partitioning
    • METIS라는 방법을 사용해서 잘리는 edge의 수와 그 edge에 붙어있는 weight을 최소화하는 방향으로 자른다. 또한, 그래프를 거의 같은 사이즈의 서브 그래프로 나누는 것이다.
    • 이를 반복하여 작은 클러스터들을 만든다.

  • Relative interconnectivity
    relative_interconnectivity 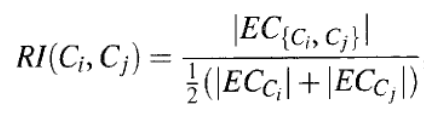각각의 클러스터의 edge cut의 평균과 새로 합쳐질 클러스터의 edge cut의 수의 상대적인 관계를 분수로 나타낸 것이다. 잘리는 edge의 수인 edge cut이 크다면 그만큼 높은 interconnectivity를 갖는 것이다.

  • Relative closeness
    relative_closeness
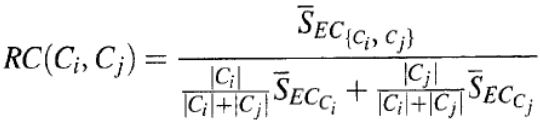
    IC는 edge cut의 수로 판단했다면, RC는 edge cut의 weight으로 판단하는 것이다. 두 클러스터의 size를 고려하여 weighted average를 하고 이 값과 새로 합쳐질 클러스터의 closeness가 얼마나 큰 가(=edge cut의 weight의 합이 얼마나 큰 가)를 나타낸 것이다.

몇 개의 클러스터를 만들 것인가는 미리 입력값으로 주어야 한다. 그것이 곧 종료 조건이 된다.

Density-Based Methods

거리만으로 클러스팅하지 않고, density를 기반으로 클러스터링하는 것을 말한다. 주요 특징으로는, 임의의 모양의 클러스터를 찾을 수 있고 noise를 처리할 수 있으며, 한 번의 스캔만으로도 효율적으로 동작한다. 또한 종료 조건으로 density parameters들이 필요하다. DBSCAN, OPTICS, CLIQUE 등의 알고리즘들이 있다.

기본적으로 두 개의 parameter가 존재한다. Eps와 MinPts인데, Eps는 maximum radius를 말하고 MinPts는 포함해야하는 최소 object의 수를 말한다. 즉, Eps를 반지름으로 하는 원이 클러스터의 범위가 되며, 그 안에는 MinPts 이상의 object가 존재하는 것이다.

NEps(p)라는 표현을 알아야 한다. 이는 점 p와 거리가 Eps 이하인 q들(점들)의 집합을 말한다.

여기서 알아야하는 개념으로 directly density-reachable이 있다.

1. Directly density-reachable 점 p가 점 q로부터 directly density-reachable하다면, 주어진 Eps와 MinPts 하에서, p는 NEps(q)에 해당하고, core point condition을 만족해야 한다.

Core point condition은 NEps(q) >= MinPts로 결국 neighbors의 수가 MinPts 이상인 경우를 말한다.

Directly density-reachable은 symmetric하지 않다. 예를 들어, p가 q의 neighbor에 속하고 q의 neighbor의 수가 MinPts 이상이라도 그 반대는 성립하지 않을 수 있는 것이다.

2. Density-reachable 어떤 점 p가 점 q로부터 density-reachable하다면, 주어진 Eps와 MinPts 하에서, p1부터 pn까지 chain이 있다는 것이다. 이 chain은 p1은 q, pn은 p이고 pi+1은 pi으로부터 directly density-reachable하다는 것을 의미한다.

3. Density-connected 어떤 점 p가 점 q로부터 density-connected하다면, 주어진 Eps와 MinPts 하에서, 어떤 점 o가 있는데 점 p와 q가 동시에 점 o로부터 density reachable한 것이다.

DBSCAN: Density Based Spatial Clustering of Applications with Noise

Density-based 알고리즘이며, 클러스터는 density-connected points의 최대 집합으로 정의된다. 노이즈가 섞여 있는 공간 데이터베이스에서 클러스터를 찾는다.

알고리즘은 다음과 같다.

1) 임의로 점 p를 고르고, p로부터 density-reachable한 점들을 모두 찾는다.
2) 만약 p가 core point라면 클러스터가 만들어지고, 그렇지 않으면 border point로 다른 점에서 다시 탐색을 시작한다.
3) 모든 point들을 방문할 때까지 반복한다. 결과적으로, Eps와 MinPts와 같은 파라미터에 따라 클러스터가 다르게 만들어진다.

DBSCAN의 문제는 파라미터에 너무 sensitive하다는 것이다. 이를 어떻게 극복할 수 있을까? OPTICS..!

OPTICS: Ordering Points To Identify the Clustering Structure

Cluster-Ordering Method로 말 그대로 점들을 ordering하는 것에서 시작한다. Density-based clustering 구조를 사용해서 DB에서 special한 object의 순서를 생성한다.

  • Core distance(of o): object o가 core point가 되도록 하는 거리
  • Reachability Distance(of p from o):
    • r(p, o) = max(core-distance(o), d(o,p))

시작점 하나를 정하여 그래프에 표기하고 reachablity distance가 아직 정의되지 않은 상태이니까 undefined로 한다. core distance를 기반으로 다른 모든 점의 reachable distance를 갱신한다. 가장 가까운 점을 두번째 점으로 하여 그래프 두번째에 표기하고 다시 두번째를 중심으로 reachable distance를 갱신하고 가장 가까운 점을 세번째 점으로 고른다. 이런식으로 계속 반복하면 Eps를 대략 정할 수 있게 되며 이를 기준으로 잘라내면 각각 클러스터가 된다.

Outlier Analysis

What is Outlier Discovery?

Outlier란 다른 데이터와 매우 다른 object들을 말한다. 매우 큰 데이터 집합에서 outlier를 정의하고 찾는 것이 주된 문제이다. 이를 통한 응용 프로그램으로는 신용카드 부정행위 감지, 의료 분석 등이 있다.

Outlier Discovery: Statistical Approaches

데이터 집합을 생성하는 기본 분포 모형(ex: 정규 분포)을 가정하고 데이터 분포, 분포 모수(평균, 분산), 예상되는 outlier의 개수 등에 따라 불일치 테스트(discordancy test)를 한다. 이렇게 하면 쉽겠지만 대부분의 테스트는 단일 attribute에 대한 것(실제는 많은 attribute를 갖고 있음)으로, 많은 경우에 데이터의 분포를 알 수 없다. 결과적으로 데이터의 분포를 잘 모른채로 할 수 있어야 한다.

Outlier Discovery: Distance-Based Approach

통계적 방법에 의해 생기는 limitations에 대응하기 위해 도입되었다. 데이터 분포를 모른채로 하는 다차원 분석이 필요한 것이다. 이를 극복하기 위한 방법이 바로 distance-based approach이다.

Distance-based outlier(DB(p, D)-outlier): 모든 페어에 대해 거리를 계산하고 p% 이상 점 o에서 D 거리 이상 떨어져 있으면 o는 outlier이다.

Distance-based outlier를 마이닝하는 알고리즘으로는 index-based, nested-loop, cell-based algorithm들이 있다.

Density-based Local Outlier Detection

Distance-based는 global distance distribution을 기반으로 하므로 데이터가 uniform하게 분포하지 않으면 힘들다. 그래서 이를 개선하기 위해 local outlier를 사용한다.

DB(p,D)-outlier 방법을 사용하면 D값을 설정해야 하는데 각 클러스터마다 떨어진 거리가 다르면 힘들어지므로 제안된 방식이다.